Заметим, что точка не лежит между двумя параллельными прямыми, а значит, фигура которая высекается прямыми будет трапецией в плоскости АD1D2, так как прямые параллельны. Посмотрим на рисунок в плоскости АD1D2 - это, как уже было сказано ранее, трапеция, но не простая. Известно равенство отрезков KC1 = C1D1. Рассмотрим ΔD1D2K.
В нем проведена прямая С1С2 ║основанию через середину стороны D1K(KC1 = C1D1), значит эта прямая - средняя линия треугольника ⇒точка C2 делит сторону пополам и, по свойству средней линии, . Находим по этой формуле C1C2. Он равен 8.5.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответсвенно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
AC = A1C1, по условию.
Так как ∠B = ∠B1, по условию => ∠А = ∠А1, так как сумма острых углов прямоугольного треугольника равна 90°.
=> △ABC = △A1B1C1 (по катету и прилежащему к нему острому углу)
ответ: 8.5
Объяснение:
Заметим, что точка не лежит между двумя параллельными прямыми, а значит, фигура которая высекается прямыми будет трапецией в плоскости АD1D2, так как прямые параллельны. Посмотрим на рисунок в плоскости АD1D2 - это, как уже было сказано ранее, трапеция, но не простая. Известно равенство отрезков KC1 = C1D1. Рассмотрим ΔD1D2K.
В нем проведена прямая С1С2 ║основанию через середину стороны D1K(KC1 = C1D1), значит эта прямая - средняя линия треугольника ⇒точка C2 делит сторону пополам и, по свойству средней линии,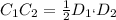
. Находим по этой формуле C1C2. Он равен 8.5.
Дано:
△ABC и △A1B1C1 - прямоугольные.
AC = A1C1
∠B = ∠B1.
Доказать: △ABC = △A1B1C1.
Решение.
Теорема.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответсвенно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
AC = A1C1, по условию.
Так как ∠B = ∠B1, по условию => ∠А = ∠А1, так как сумма острых углов прямоугольного треугольника равна 90°.
=> △ABC = △A1B1C1 (по катету и прилежащему к нему острому углу)
Ч.Т.Д.