Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 = (кв.ед.)
Из формулы площади шестиугольника S= выражаем сторону а:
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)
https://tex.z-dn.net/?f=S_%7BABD%7D%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20AD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%5C%5C%5C%5CS_%7BCBD%7D%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20CD%5Ccdot%20BD%5Ccdot%20%5Csin%7B(180%5E%7B%5Ccirc%7D-%5Calpha)%7D%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20CD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%5C%5C%5C%5C%5Cfrac%7BS_%7BCBD%7D%7D%7BS_%7BABD%7D%7D%3D%5Cfrac%7B1%2F2%5Ccdot%20%5Ccdot%20CD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%7D%7B1%2F2%5Ccdot%20AD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%7D%3D%5Cfrac%7BCD%7D%7BAD%7D%3D%5Cfrac%7B13x%7D%7B2x%7D%5C%5C%5C%5CS_%7BCBD%7D%2BS_%7BABD%7D%3D75%3D15x%5CRightarrow%20x%3D5%5C%5C%5C%5CS_%7BABD%7D%3D2x%3D10%5C%5C%5C%5COtvet%5C!%5C!%3A%5C%3B10.
Объяснение:
Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 =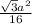
(кв.ед.)
Из формулы площади шестиугольника S=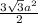
выражаем сторону а:
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)