в равнобедреном треугольнике АВС отрезок АD- медиана проведена к оснаванию. на сторонах АВ и АС отмечены соответствено точки М и К так что ВМ=СК докажите равенство треугольника АМDи АКD
Через две образующие конуса проведена плоскость, которая наклонена к основанию под углом углом α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Найдите площадь боковой поверхности конуса, если его образующая равна m
Объяснение:
1) Пусть МА=МВ=m -образующие конуса, МО-высота конуса, МО⊥(АОВ) АВ-хорда , ∠АОВ=β. Проведем ОН⊥АВ , тогда МН⊥АВ , по т. о трех перпендикулярах ⇒ ∠МНО-линейный угол между основанием и плоскостью (АВМ), ∠МНО=α .
2) S(бок.конуса )= π * r* l . где r-радиус основания, l-образующая конуса. По условию l =m . Найдем r.
3)В равнобедренном ΔАОВ, высота является биссектрисой ⇒∠АОН=β/2. Получили ΔАОН- прямоугольный :
,
.
4) ΔMHO- прямоугольный : или .
5) ΔAMH- прямоугольный ,по т. Пифагора НА²+МН²=МА² ,
1) Центром вписанной окружности треугольника является точка пересечения биссектрис.
Биссектриса к основанию равнобедренного треугольника является высотой и медианой.
MO - биссектриса, KE - биссектриса, высота и медиана.
ME=EN=10
По теореме Пифагора
KE =√(MK^2-ME^2) =12*2 =24
По теореме о биссектрисе
KO/OE =MK/ME =13/5 => OE =5/18 KE =20/3
Или по формулам
S=pr
S=√[p(p-a)(p-b)(p-c)], где p=(a+b+c)/2
Отсюда
r=√[(p-a)(p-b)(p-c))/p]
при a=b
r=c/2 *√[(a -c/2)/(a +c/2)] =10*√(16/36] =20/3
3) Вписанный угол, опирающийся на диаметр - прямой, K=90
MN =2*OM =26
По теореме Пифагора
KN =√(MN^2-MK^2) =5*2 =10
P(KMN) =2(5+12+13) =60
Через две образующие конуса проведена плоскость, которая наклонена к основанию под углом углом α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Найдите площадь боковой поверхности конуса, если его образующая равна m
Объяснение:
1) Пусть МА=МВ=m -образующие конуса, МО-высота конуса, МО⊥(АОВ) АВ-хорда , ∠АОВ=β. Проведем ОН⊥АВ , тогда МН⊥АВ , по т. о трех перпендикулярах ⇒ ∠МНО-линейный угол между основанием и плоскостью (АВМ), ∠МНО=α .
2) S(бок.конуса )= π * r* l . где r-радиус основания, l-образующая конуса. По условию l =m . Найдем r.
3)В равнобедренном ΔАОВ, высота является биссектрисой ⇒∠АОН=β/2. Получили ΔАОН- прямоугольный :
4) ΔMHO- прямоугольный :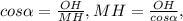 или
или 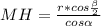 .
.
5) ΔAMH- прямоугольный ,по т. Пифагора НА²+МН²=МА² ,
r =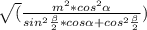 =
= 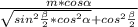 .
.
6) S(бок.конуса )= π *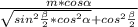 *m
*m
S(бок.конуса )=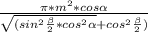 ( ед²) .
( ед²) .