В тетради записать номера утверждений и отметить: знаком « + » верные утверждения,
знаком « - » неверные утверждения.

1) Начальные геометрические сведения
(отрезки, прямые и углы).
1. Существуют три прямые, которые проходят через одну точку.
2. Смежные углы всегда равны.
3. Вертикальные углы равны.
4. Всегда один из двух смежных углов острый, а другой тупой.
5. Через заданную точку плоскости можно провести только одну прямую.
6. Если угол острый, то смежный с ним угол также является острым.
7. Через две различные точки на плоскости проходит единственная прямая.
8. Сумма смежных углов равна 180°.
2) Параллельные и перпендикулярные прямые.
1. Две прямые, параллельные третьей прямой, перпендикулярны.
2. Две прямые, перпендикулярные третьей прямой, перпендикулярны.
3. Две различные прямые, перпендикулярные третьей прямой, параллельны.
4. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
5. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
6. Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
7. Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
8. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти две прямые параллельны.
9. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
10. Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то эти две прямые параллельны.
11. Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равны 180°, то эти две прямые параллельны.
3) Треугольник.
1. Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
2. В любом тупоугольном треугольнике есть острый угол.
3. В тупоугольном треугольнике все углы тупые.
4. В треугольнике против большего угла лежит большая сторона.
5. Внешний угол треугольника больше не смежного с ним внутреннего угла.
6. Внешний угол треугольника равен сумме его внутренних углов.
7. Медиана треугольника делит пополам угол, из вершины которого проведена.
8. Один из углов треугольника всегда не превышает 60 градусов.
9. Сумма углов любого треугольника равна 360 градусам.
10. Треугольник со сторонами 1, 2, 4 существует.
13. Биссектриса треугольника делит пополам сторону, к которой проведена.
14. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
15. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
16. Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
17. Всякий равнобедренный треугольник является остроугольным.
18. Каждая из биссектрис равнобедренного треугольника является его высотой.
19. Каждая из биссектрис равнобедренного треугольника является его медианой.
20. Сумма углов равнобедренного треугольника равна 180 градусам.
21. Все высоты равностороннего треугольника равны.
22. Всякий равносторонний треугольник является равнобедренным.
23. Всякий равносторонний треугольник является остроугольным.
24. В прямоугольном треугольнике гипотенуза равна сумме катетов.
25. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
26. Сумма углов прямоугольного треугольника равна 90 градусам.
27. Сумма острых углов прямоугольного треугольника равна 90 градусам.

Показать ответ

Ответ:

Grotesk1077

19.03.2021 07:11

Задача решается проще, если вспомнить, что медианы в точке пересечения (т. е. все три медианы в любом треугольнике пересекаются внутри него строго в одной точке - это центр тяжести треугольника). Так вот эти медианы делятся в точке пересечения в соотношении 2 к 1, считая от вершины. Значит ВО=15*2/3=30/3=10 см, СО=18*2/3=6*2=12 см.

ОВ1=15/3=5 см, ОС1=18/3=6 см. Теперь нужно вспомнить теорему Пифагора. Треугольник ВОС - прямоугольный, значит ВС - гипотенуза.

BC^2=BO^2+OC^2

BC^2=10^2+12^2

BC^2=100+144

$BC=\sqrt{244}$

Треугольник ВОС1 - тоже прямоугольный, так как угол С1OB - прямой. Доказывается так.

$\angle COC_1=\angle C_1OB+\angle BOC$

$\angle COC_1=180^0$ - как развернутый угол.

$180^0=\angle C_1OB+90^0$

$\angle C_1OB=180^0-90^0$

$\angle C_1OB=90^0$

По теореме Пифагора из треугольника находим гипотенузу ВС1.

BC_1^2=C_1O^2+BO^2

BC_1^2=6^2+10^2

$BC_1=\sqrt{136}$

Заметим, что BC1 - половина АВ по определению медианы СС1.

$AB=2\sqrt{136}$

Треугольник B1OC - прямоугольный, так как угол B1OC - прямой, как вертикальный к углу С1OB. Та же теорема Пифагора, чтобы вычислить гипотенузу В1С.

B_1C^2=OB_1^2+OC^2

B_1C^2=12^2+5^2

B_1C^2=144+25

B_1C^2=169

B1C=13 см.

Заметим также, что В1С - половина АС. Значит АС=26 см.

Вычислим периметр АВ.

$P_{\Delta ABC}=26+2\sqrt{136}+\sqrt{244}$

0,0(0 оценок)

Ответ:

tarasgorodchukowd1fp

04.11.2022 23:57

Дано:

Правильная четырёхугольная пирамида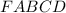 FABCD .

AB=6 (см).

FG=7 (см).

Найти:

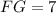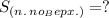$S_{(n. \: no_Bepx.)}=?$ (см²).

Решение:

$\boxed{S_{(n. \: no_Bepx.)}=S_{(oc_Ho_B.)}+S_{(6o_K. \: no_Bepx.)}}$

Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.

В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому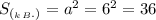 $S_{(_k_B.)}=a^2=6^2=36$ (см²).

Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.

Значит нам нужно сначала найти апофему нашей пирамиды.

1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.

Объяснение 1 правила: из этого следует, что апофема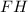 делит сторону основания 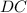так, что 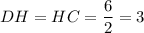$DH=HC=\dfrac{6}{2}=3$ (см).

Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный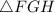 $\triangle FGH$ , где 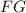- катет прямоугольного тр-ка (высота пирамиды); 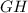- катет прямоугольного тр-ка; 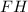- гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что 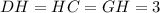DH=HC=GH=3 (см).

Так как апофема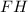 нашей пирамиды является ещё и гипотенузой прямоугольного 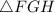$\triangle FGH$ , то мы сможем найти её величину по т.Пифагора:

$FH=\sqrt{FG^2+GH^2}=\sqrt{7^2+3^2}=\sqrt{49+9}=\sqrt{58}$ (см).

Теперь найдём периметр основания (квадрата):

$P=4a=6\cdot4=24$ (см).

Затем найдём площадь боковой поверхности:

$S_{(6ok. \: no_B.)} =P_{(oc_Ho_B.)}\cdot\dfrac{1}{2}\cdot FH=24\cdot\dfrac{1}{2}\cdot\sqrt{58}=12\sqrt{58}$ (см²).

Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"

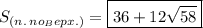$S_{(n. \: no_Bepx.)}=\boxed{36+12\sqrt{58}}$ (см²).

ответ: $\boxed{S_{(n. \: no_Bepx.)}=36+12\sqrt{58}}$ (см²).
Вправильной четырехугольной пирамиде сторона основания равна 6 см, а высота пирамиды равна 7см. вычи