В трапеции ABCD с основаниями АВ и CD диагонали пересекаются в точке Е. Площадь треугольника АВЕ равна 72, площадь треугольника CDE равна 50. Найдите площадь трапеции ABCD.
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её ). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме и , то есть
242
Объяснение:
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её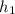
). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме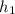
и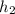 
, то есть