В треугольник MPK вписана окружность, O - ее центр, ∠M = 50°, ∠K = 70°.
Вычислите градусные меры углов MOK, MOP, POK.
Решение.
Рассмотрим треугольники MOK, MOP, POK. O - центр окружности, вписанной в треугольник MPK, значит, O - точка пересечения этого треугольника. Поэтому ∠OMK = ∠OMP °, ∠OKP = ∠OKM = ° . Теперь найдем угол P. ∠P = ° - (° +°) = ° . Значит, ∠MPO
вот фото.
Так как площадь боковой повехности призмы вычисляется по формуле:
Так как площади боковых поверхностей равны, и равны высоты получаем равенство периметров оснований данных призм:
Площадь полной поверхности призмы численно равна сумме площадей оснований и боковой поверхности:
Так как известно что разность полных площадей равна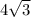 получаем:
получаем:
Получаем:
ответ: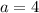 - сторона основания трехгранной призмы
- сторона основания трехгранной призмы
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.
Исходя из этого св-ва найдем их полусумму, которая так же является сумой катетов любого из п/у треугольников, образованных этими диагоналями:
d1+d2=61
(d1+d2)/2=31
d1=x; d2=(31-x)
Теперь расмотрим любой из этих треугольников. Зная, что сторона ромба (она же гипотенуза) равна 25, то составим уравнение на основе теоремы Пифагора:
625=x^2 +(31-x)^2
2x^2-62x+336=0
x^2-31x+168=0
D=289;
x1=7
x2=24
Ну так как 31-7=24, то катеты будут 24см и 7см
Диагонали будут в 2 раза длиннее, т.е. 48см и 14см
Площадь ромба через полупроизведение диагоналей:
S=48*14*1/2=336(см2)
ответ: 336 (см2)