Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
, тогда а= .
По т. Пифагора а²+b²=(3+4)² ,( )²+b²=49 ,
+b²=49 , 9b²+16b²=49*16 , b²= , b== 5,6 (см)
a= =4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
По т. Пифагора а²+b²=(3+4)² ,(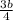 )²+b²=49 ,
)²+b²=49 ,
a=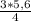 =4,2 cм
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
Объяснение:
1)
Проведём две высоты ВК и CL
sin30°=BK/AB
BK=AB*sin30°=4*1/2=2
cos30°=AK/AB
AK=AB*cos30°=4*√3/2=2√3
АК=LD
BC=KL
AD=2*AK+KL=2*2√3+√3=5√3
S(ABCD)=BK(BC+AD)/2=2(√3+5√3)/2=6√3
ответ: площадь трапеции равна 6√3.
2)
∆LMO- прямоугольный, равнобедренный треугольник LO=MO
LO=LM/√2=6/√2=3√2/√2=3√2.
OB=MN
LK=2*LO+OB=2*3√2+2√2=8√2.
S(LMNK)=MO(MN+LK)/2=3√2(2√2+8√2)/2=
=3√2*10√2/2=15*2=30
ответ: площадь трапеции равна 30
3)
sin60°=BK/AB
BK=AB*sin60°=7*√3/2=3,5√3
cos60°=AK/AB
AK=AB*cos60°=7*1/2=3,5
AD=2*AK+BC=2*3,5+4=11
S(ABCD)=BK(BC+AD)/2=3,5√3(4+11)/2=
=3,5√3*15/2=26,25√3
ответ: площадь трапеции равна 26,25√3