в треугольнике abc точки d и m принадежат сторонам ab и bc dm и ac параллельны докажи что треугольник bdm подобен треугольнику abc

Показать ответ

Ответ:

daeinam095

18.02.2020 08:00

Случай 1 : Площадь бо́льшего треугольника равна 8 (ед²).Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.

Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).

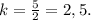
$k = \frac{5}{2} = 2,5.$

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Отсюда -

$\frac{S_{1} }{S_{2} } = k^{2} \\\\\frac{8}{S_{2} } = 2,5^{2} \\\\\frac{8}{S_{2} } = 6,25\\\\S_{2} = \frac{8}{6,25} \\\\\boxed{S_{2} = 1,28}$

1,28 (ед²).

- - -

Случай 2 - Площадь меньшего треугольника равна 8 (ед²).

В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).

S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника

Тогда -

$k = \frac{2}{5} = 0,4.$

$\frac{S_{2} }{S_{1} } = k^{2}\\\\\frac{8 }{S_{1} } = 0,4^{2}\\\\\frac{8 }{S_{1} } = 0,16\\\\S_{1} = \frac{8}{0,16}\\\\\boxed{S_{1} = 50}$

50 (ед²).

0,0(0 оценок)

Ответ:

owl2006owl

18.12.2020 00:46

Задание сводится к тому, чтобы провести окружность с центром в вершине угла и радиусом, равным четверти отрезка.
Дано:
угол О;
отр АВ
Построить
ГМТ, равноудаленных от т О на расстояние равное 1/4 АВ

Построение:
1) точка А
2) окр1 (А; АВ)
3) окр2 (В, АВ)
4) окр1 пересек окр 2 в точках К и К1
5) КК пересекает АВ в точке М
6) окр3 (А; АМ)
7) окр4 (М; АМ)
8) окр 3 пересекает окр 4 в точках Р и Р
9) РР1 пересекает АВ в точке С, АС = 1/4 *АВ
10) окр5 (О; АС) - ГМТ, равноудаленных от вершины угла на расстояние 1/4*АВ.

0,0(0 оценок)

Популярные вопросы: Геометрия