В треугольнике abc угол a = 66 градусам, угол c = 47 градусам, bd - биссектриса угла abc. через вершину b проведена прямая mn || ac. найдите угол mbd. С рисунком:)
1)Чтобы найти площадь боковой поверхности призмы нужно найти площадь одного прямоугольника (6*9=54) и умножить на количество прямоугольников (54*4=216) Площадь боковой поверхности равен 216 см^2
Площадь всей поверхности равна сумме площади оснований (в основании лежит квадрат и его площадь равна =36 и умножаем на 2, т.к их два 36*2=72) и боковой поверхности (216+72=288) Площадь всей поверхности призмы равна 288 см^2.
2) С теоремы пифагора находим половину стороны квадрата, лежащего в основании пирамиды. (
Находим площадь одного треугольника (S=1/2*a*h, где а-сторона квадрата, h- высота треугольника(в данной задаче, апофема)
S=1/2*16*10=80 и умножаем на кол-во треугольников 80*4=320см^2
3) Чертим диагональ в основании, и диагональ основания, диагональ призмы и ребро призмы образуют прямоугольный треугольник, который будет является и равнобедренным, т.к два угла будут равны (45+x+90=180, x=45)
Находим диагональ прямоугольника по теореме пифагора (,это и будет являться высотой призмы.
Находим площади боковых прямоугольников и складываем (6*10+6*10+8*10+8*10=280см^2) Площадь боковой поверхгости призмы равно 280 см^2.
1)216 cm^2 и 288 cm^2 2)320 cm^2 3)280 cm^2
Объяснение:
1)Чтобы найти площадь боковой поверхности призмы нужно найти площадь одного прямоугольника (6*9=54) и умножить на количество прямоугольников (54*4=216) Площадь боковой поверхности равен 216 см^2
Площадь всей поверхности равна сумме площади оснований (в основании лежит квадрат и его площадь равна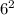
=36 и умножаем на 2, т.к их два 36*2=72) и боковой поверхности (216+72=288) Площадь всей поверхности призмы равна 288 см^2.
2) С теоремы пифагора находим половину стороны квадрата, лежащего в основании пирамиды. (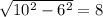
Находим площадь одного треугольника (S=1/2*a*h, где а-сторона квадрата, h- высота треугольника(в данной задаче, апофема)
S=1/2*16*10=80 и умножаем на кол-во треугольников 80*4=320см^2
3) Чертим диагональ в основании, и диагональ основания, диагональ призмы и ребро призмы образуют прямоугольный треугольник, который будет является и равнобедренным, т.к два угла будут равны (45+x+90=180, x=45)
Находим диагональ прямоугольника по теореме пифагора (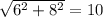
,это и будет являться высотой призмы.
Находим площади боковых прямоугольников и складываем (6*10+6*10+8*10+8*10=280см^2) Площадь боковой поверхгости призмы равно 280 см^2.
№1 a - катет, b - катет, с - гипотенуза.
sin45° = a/c
a = c * sin45° = (18 * √2)/2 = 9√2 (см)
a = b = 9√2 (см)
№2
S = a² * sin50° = 4 * 0.76 = 3.04 (см²)
№3 Тут некрасивые числа, поэтому я не хочу решать)
№4 a - катет, b - катет, с - гипотенуза.
sin∠α = a/c = 15/25 = 0.6 (в таблице брадиса 0.6 равен 37°)
cos∠β = a/c = 15/25 = 0.6 ( 53° )
ответ: 53° и 37°
№5
ответ: А, Г
№6 ABCD - прям. АС - диагональ, ∠CAD = 40°
cos40° = AD/AC
AD = AC * cos40° = 12 * 0.76 = 9.12 (см)
sin40° = CD/AC
CD = AC * sin40° = 12 * 0.64 = 7.68 (см)
P = 2*(AD+CD) = 2*(9.12+7.68) = 2 * 16.8 = 33.6 (см)
№7 ABCD - трап. BK - высота.
В трапеции в которую можно вписать круг, сума боковых сторон, равна суме оснований.
AB + CD = BC + AD
Далее за теоремой Пифагора:
AB² = BK² + AK²
AK = √AB²-BK² = √17²-8² = √289-64 = √225 = 15 (см)
Проводим с точки C такую же высоту к основе (высота CN)
ND = AK
BC + AD = 17*2 = 34 (см)
BC + KN = BC + AD - 2AK = 34 - 2 * 15 = 4 (см)
BC = KN
BC = 4/2 = 2 (см)
ответ: 2 см...