в треугольнике АВК проведена биссектриса ВК, угол А=15°, угол С=55°. а) доеажите что треугольник АВС равнобедренный б) сравните отрезки ВК и КС​

На рисунке 20.4 укажите равновеликие параллелограммы

1 ВАРИАНТ

Фигуры, имеющие равную площадь, называются - равновеликими. Проверим это ниже.

формула площади параллелограмма выглядит следующим образом:

S=ah, где а-основание, h-высота.

Пусть 1 клетка равняется 1см, тогда:

б)  a=1,5см, h=4см;

S=1,5*4=6(см²)

в) а=3см, h=3см

S=3*3=9(см²)

г) a=3см, h=2см

S=3*2=6(cм²)

д) а=2см, h=3см

S=2*3=6(см²)

ж) а=2см, h=4см

S=2*4=8(см²)

и) а=6см, h=2см

S=6*2=12(см²)

Вывод: равновеликими параллелограммами будут б),г),д).

ответ: б),г),д)

2 ВАРИАНТ

прямоугольник - это частный случай параллелограмма

формула площади прямоугольника:

S=ab, где а-сторона, b-сторона

а) а=1см, b=8см

S=1*8=8(см²)

б)  a=1,5см, h=4см;

S=1,5*4=6(см²)  

в) а=3см, h=3см

S=3*3=9(см²)

г) a=3см, h=2см

S=3*2=6(cм²)

д) а=2см, h=3см

S=2*3=6(см²)  

е) а=2см, b=3см

S=2*3=6(см²)

ж) а=2см, h=4см

S=2*4=8(см²)

з) а=4см, b=2см

S=4*2=8(см²)

и) а=6см, h=2см

S=6*2=12(см²)

Вывод: равновеликими параллелограммами будут б),г)д),е) и  а),ж),з)

ответ: б),г)д),е) и  а),ж),з)

Точки М i Р лежать відповідно на сторонах АB i BC трикутника АВС, АВ* РВ=СB*МB. Доведіть, що МР паралельна АC.

Объяснение:

АВ* РВ=СB*МB /: СВ*РВ ,

,  .

По второму признаку подобия : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника (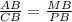 )   и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС