На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH= , FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)
На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH=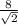 , FH=4√2 см=0,04√2 м
, FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)
На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH=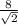 , FH=4√2 см=0,04√2 м
, FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)