Т.к. RE=ES=TF=FQ ⇒ RS=TQ ⇒ RSQT- равнобедренная трапеция.
Для равнобедренной трапеции справедливо (*).
Из прямоугольного ΔRKS найдем RK : тк один из острых углов 45°, то и другой острый угол 45°⇒ ΔRKS- прямоугольный равнобедренный ⇒SK=RK=8. Получаем или RT=26 .
EF-средняя линия , т.к. по условию она проходит через середины сторон RS ,TQ ⇒ EF=
=================================
(*) Высота , опущенная из вершины на большее основание , делит его на большой отрезок , который равен полусумме оснований и меньший- равен полуразности оснований.
1 зд
C и D
B и F
2 зд
AB = A1B1, AC = A1C1, BC = B1C1
3 зд
28
4 зд
Пусть NT не является биссектрисой угла MNK.
Тогда ∠MNT ≠ ∠KNT.
По условию задачи MN = KN и MT = KT.
Отрезок NT – общая сторона треугольников MNT и KNT.
Тогда получается, что ΔMNT = ΔKNT по третьему признаку равенства треугольников.
Из равенства треугольников следует, что ∠MNT = ∠KNT.
Получено противоречие.
Следовательно, NT является биссектрисой угла MNK.
5 зд
BDC = 48°
AB = BD
по третьему признаку равенства треугольников ΔABC = ΔDBC
AC = CD
AB = 1,5 м
6 зд
ответ 37,5
7 зд
Так как BK = 14 см, то AB = 50 – (14 + 15) = 50 – 29 = 21 см.
AB = BC
Так как BK = 14 см, то BC = 50 – (14 + 15) = 50 – 29 = 21 см.
PΔCBK = CB + BK + KC = 50 см
Так как BK – медиана, то AK = KC = AC : 2 = 30 : 2 = 15 см.
PΔABK = AB + BK + KA = 50 см
Значит, треугольник ABC – равнобедренный.
ΔABK = ΔCBK по третьему признаку равенства треугольников
8 зд
везде 180 градусов
9 зд
BF=48
FE=24
Длина окантовачной тесьмы=3•АВ=144
Периметр ABCD=4•AB=192
Для изготовления пяти воздушных змеев=720
Лишние данные=960
Площадь=1152
Объяснение:
воть
Дано: RSQT-трапеция , ∠SRK=∠QTK=45°,RE=ES=TF=FQ, SQ=10 ,SK=8, SK⊥RT. Найти: RT,EF.
Объяснение:
Т.к. RE=ES=TF=FQ ⇒ RS=TQ ⇒ RSQT- равнобедренная трапеция.
Для равнобедренной трапеции справедливо
(*).
Из прямоугольного ΔRKS найдем RK : тк один из острых углов 45°, то и другой острый угол 45°⇒ ΔRKS- прямоугольный равнобедренный ⇒SK=RK=8. Получаем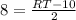
или RT=26 .
EF-средняя линия , т.к. по условию она проходит через середины сторон RS ,TQ ⇒ EF=
=================================
(*) Высота , опущенная из вершины на большее основание , делит его на большой отрезок , который равен полусумме оснований и меньший- равен полуразности оснований.