ів Із точок A, B і C, розміщених по один бік від площини α, проведені прямі, перпендикулярні до площини α. Ці прямі перетинають пряму а площини α в точках D, E і F відповідно. Знайдіть довжину відрізка BE, якщо AD = 6 см, CF = 9 см, DE = EF.
2. прямую можно обозначать одной маленькой латинской буквой (a,b,
или двумя заглавными латинскими буквами, если этими буквами обозначены точки, расположенные на прямой (ab, cd)
3. у прямой много свойств: через одну точку можно провести бесконечно много прямых, через любые две точки можно провести только одну прямую, у любой прямой, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие
4. прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения прямых называют пересекающимися.
6. утверждение, имеющее доказательство, т.е. его надо доказать.
9. их тоже несколько (равные отрезки имеют равные длины, часть отрезка всегда имеет длину, которая меньше длины отрезка, если точки на отрезке делят отрезок на части, то длина отрезка равна сумме длин этих частей.
10. длина отрезка.
11.это точка, которая делит данный отрезок на две равные части.
Но если прямые перпендикулярные (прямые, при пересечении которых образуются 4 прямых угла), то наименьший угол - это величина прямого. Но в данной задаче этого не уточняется, поэтому верный ответ - величина острого угла.
ответ:
объяснение:
2. прямую можно обозначать одной маленькой латинской буквой (a,b,
или двумя заглавными латинскими буквами, если этими буквами обозначены точки, расположенные на прямой (ab, cd)
3. у прямой много свойств: через одну точку можно провести бесконечно много прямых, через любые две точки можно провести только одну прямую, у любой прямой, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие
4. прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения прямых называют пересекающимися.
6. утверждение, имеющее доказательство, т.е. его надо доказать.
9. их тоже несколько (равные отрезки имеют равные длины, часть отрезка всегда имеет длину, которая меньше длины отрезка, если точки на отрезке делят отрезок на части, то длина отрезка равна сумме длин этих частей.
10. длина отрезка.
11.это точка, которая делит данный отрезок на две равные части.
1)
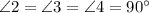; 2) Величина острого (наименьшего) угла.
Объяснение:1) Начертим две пересекающие прямые. Обозначим их буквами
и 
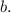
При их пересечении, образовался угол в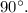
Пусть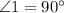
Вертикальные углы равны.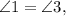
как вертикальные.
Сумма смежных углов равна2) Угол между двумя пересекающимися прямыми - это величина наименьшего угла между двумя пересекающимися прямыми.
Обозначим две пересекающиеся прямые буквами
и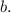 
При пересечении произвольных прямых, образуются 4 угла: 2 равных тупых угла и 2 равных острых угла (они равны, как вертикальные).
В данном случае наименьший угол - это величина острого угла, так как величина острого угла меньше тупого.
=============================================================
Но если прямые перпендикулярные (прямые, при пересечении которых образуются 4 прямых угла), то наименьший угол - это величина прямого. Но в данной задаче этого не уточняется, поэтому верный ответ - величина острого угла.