Сторона описанного правильного треугольника на √6 больше стороны правильного четырёхугольника, вписанного в ту же окружность. Найти сторону треугольника.
Правильный четырехугольник - квадрат, и диаметром окружности, в которую он вписан, является его диагональ.
Обозначим вписанный квадрат КОМН
Пусть его стороны=а.
Тогда диаметр РН описанной вокруг него окружности равен а√2,
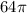 см³.
см³.
Объяснение:Обозначим данную пирамиду буквами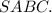
Проведём высоту пирамиды SO.
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
Проведём высоту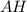 в
в 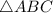
Так как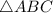 - равносторонний ⇒
- равносторонний ⇒ 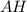 - высота, медиана и биссектриса
- высота, медиана и биссектриса
Найдём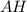 по теореме Пифагора
по теореме Пифагора 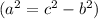 .
.
Точка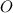 - пересечение медиан и делит их в отношении
- пересечение медиан и делит их в отношении 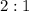 , считая от вершины.
, считая от вершины.
Также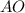 - радиус описанной около
- радиус описанной около 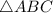 окружности.
окружности.
Рассмотрим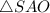
Если угол в прямоугольном треугольнике равен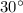 , то напротив лежащий катет равен половине гипотенузы.
, то напротив лежащий катет равен половине гипотенузы.
Составим уравнение:
Пусть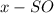 , тогда
, тогда  .
.
И по теореме Пифагора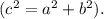
Сторона описанного правильного треугольника на √6 больше стороны правильного четырёхугольника, вписанного в ту же окружность. Найти сторону треугольника.
Правильный четырехугольник - квадрат, и диаметром окружности, в которую он вписан, является его диагональ.
Обозначим вписанный квадрат КОМН
Пусть его стороны=а.
Тогда диаметр РН описанной вокруг него окружности равен а√2,
радиус ОН=а√2):2=a/√2
Стороны описанного треугольника АВС=а+√6
Радиус ОН вписанной в него окружности =ВН/3
ВН=АВ*sin 60º=√3*(а+√6):2
OH=√3*(а+√6):6
Приравняем оба значения ОН:
a/√2=√3*(а+√6):6 из чего следует
а=(а+√6):√6⇒
a=√6:(√6-1)
АВ=[√6:(√6-1)]+√6
АВ=(√6+6-√6):(√6-1)=6:(√6-1)