Вариант-2. 1. Диагонали прямоугольника MNKP пересекаются в точке 0, L MON=64°.
Найдите угол ОМР.
2. Найдите углы равнобедренной трапеции, если один из его углов на 30° больше
другого.
3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см.
Найдите стороны параллелограмма.
4. В прямоугольной трапеции разность углов при одной из боковых сторон равна
48°. Найдите углы трапеции.
Объяснение:
Площадь боковой поверхности прямого параллелепипеда:
S = Росн · ВВ₁
Росн = 2(AB + BC) = 2(1 + 7√3)
Проведем ВН⊥АС. ВН - проекция В₁Н на плоскость основания, значит
В₁Н⊥АС по теореме о трех перпендикулярах, ⇒
∠В₁НВ = 60° - линейный угол двугранного угла между плоскостями (В₁АС) и основанием.
ΔАВС: по теореме косинусов:
АС² = AB² + BC² - 2·AB·BC·cos∠B
AC² = 1 + 147 + 2 · 7√3 · √3/2 = 148 + 21 = 169
AC = 13
Sabc = 1/2 AB · BC · sin∠B = 1/2 · 7√3 · 1/2 =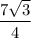
Sabc = 1/2 AC · BH
ΔBB₁H:
tg∠B₁HB = BB₁ / BH
BB₁ = BH · tg60°
ABCD - параллелограмм, AB = CD = 4 см, AD = BC = 6 см, угол BAD = 30 градусов. Из вершины В проведем к стороне AD высоту ВН.
Рассмотрим треугольник AHB: угол АНВ = 90 градусов, так как ВН - высота, угол ВАН = угол BAD = 30 градусов, АВ = 4 см - гипотенуза, так как лежит напротив прямого угла, АН и ВН - катеты.
Из свойств прямоугольного треугольника: катет, лежащий напротив угла, равного 30 градусов, равен половине гипотенузы.
В треугольнике АНВ напротив угла ВАН лежит катет ВН, тогда: ВН = АВ/2 = 4/2 = 2 (см). Площадь параллелограмма находится по формуле: S = ah, где а - сторона параллелограмма, h - высота, проведенная к стороне а. S = AD*BH = 6*2 = 12 (см^2). ответ: S = 12 см^2.