Вариант 2 1. Диагонали прямоугольника MNKP пересекаются в точке 0, ZMON
- 59°. Найдите угол ОМР.
2. Найдите углы равнобокой трапеции, если один из ее углов на 10-
больше второго.
3. Стороны гараллелограмиа относятся как 3:1, а его периметр
ранен 56 см. Найдите стороны параллелограмма.
4. В прямоугольной трапеции разность углов при одной из боковых
сторон равна 44°. Найдите углы трапеции,
5. Высота вм, провсдоговая из вершитгы утла ромба ABCD образуст
со стороной AB угол 30°, длина диагонали AC равна 12 см.
Ilайдите AM, если точка M лежит на продолжении стороны AD.
На 5
6. В четырехугольнике сума углов, прилежащих к каждой из двух
смежных сторон, равна 1 Вр”. Докажите, что ABCD -
параллелограми.
Объяснение:
Дано:
AF и BD - прямые
AB = BС
∠АВС = 120°
АС - биссектриса ∠ВАЕ
∠CDE : ∠AED = 7 : 8
∠ DEF - ?
1) Сумма всех углов Δ = 180°:
∠ВАС + ∠В + ∠ВСА = 180° или
∠ВАС + ∠ВСА = 180° - 120° = 60°
2) ΔАВС - равнобедренный, т.к. АВ = ВС по условию.
В равнобедренном треугольнике углы при основании равны. Значит,
∠ВАС = ∠ВСА = 60° / 2 = 30°
3) АС - биссектриса ∠А по условию, следовательно,
∠ВАС = ∠ САЕ = 30°, а ∠ВАЕ = 2* 30° = 60°
4) ∠ВАЕ и ∠ АВС - односторонние углы, их сумма = 120° + 60° = 180°
Теорема: Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны, значит,
АЕ ║BD
5) ∠CDE и ∠AED - тоже углы односторонние, и так как АЕ ║BD, то
∠CDE + ∠AED = 180° или
7х + 8х = 180° → х = 180°/15 = 12°
∠CDE = 7*12° = 84°
∠AED = 8 * 12 = 96°
6) ∠CDE = ∠DEF = 84°, так как они накрест лежащие углы при параллельных прямых BD и AE/
(см. объяснение)
Объяснение:
Перед нами уравнение квадрата, точка пересечения диагоналей которого имеет координаты (0; 0) и расстояние от точки пересечения диагоналей которого до одной из вершин равно 4.
Зная это, построим график:
(см. прикрепленный файл)
Задание выполнено!
Комментарий 1:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой: либо y=-x+4, либо y=-x-4, либо y=x-4, либо y=x+4. Строим их до пересечения, таким образом получая график.
Комментарий 2:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой, причем точки "склеивания" будут в координатах (0; 4), (4; 0), (-4; 0), (0; -4). Тогда соединим их и получим график.
Комментарий 3:
При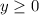 получим график модуля
получим график модуля 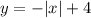 .
.
При будет
будет 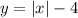 .
.
Строим это и получаем график.