Вариант 2 5. В треугольнике MNP точка Клежит на стороне MN, причем угол NKP острий. Докажите, что
KP - MP
6. Найдите углы треугольника ABC, если угол В на 40° больше угла А, угол C в пять раз больше
угла А.
7
8.
В прямоугольном треугольнике ABC (ZC = 90°) биссектрисы CD и AE пересекаются в точке 0,
ZAOC = 105°. Найдите острые углы треугольника ABC.
* Один из внешних углов треугольника в два раза больше другого внешнего угла. Найдите
разность между этими внешними углами, если внутренний угол треугольника, не смежный с
указанными внешними углами, равен 60°.
ответ: 1. Ставишь точку в начале чертишь линию, и потом ставишь точку в конце. 2. Ставишь точку в начале и чертишь линию, точку в конце ставить не надо. 3. Просто чертишь линию и всё. 4. Чертишь круг циркулем и обозначаешь центр и радиус. 5. Чертишь отрезок и обозначаешь О как начало, а А как конец. 6. Чертишь любой острый угол и строишь биссектрису, что такое биссектриса посмотри в интернете. 7. Чертишь прямой угол и строишь биссектрису, что такое биссектриса посмотри в интернете. 8. Чертишь тупой угол и строишь биссектрису, что такое биссектриса посмотри в интернете. 9. Начерти отрезок АВ любой длины, найди его середину и раздели его по серединке.
Не благодарите
Если что то не правильно то простите
26.8
Объяснение:
Выполним рисунок. (см. Рис. 1)
Прямоугольная трапеция ABCD, меньшее основание BC=5, большее основание DA=7.4, AC -биссектриса ∠С, AB⊥BC, AB⊥DA, DA║BC.
∠ACD=∠ВСА т.к. АС- биссектриса,
∠DAC=∠ВСА, как накрест лежащие, значит ∠ACD=∠DAC=∠ВСА.
ΔACD-равнобедренный, т.к. ∠ACD=∠DAC. Тогда AD=CD=7.4.
Выполним дополнительное построение (см. Рис. 2). Проведем высоту DO в ΔACD. Т.к. ΔACD-равнобедренный, то DO также является медианой, значит, AO=OC.
Пусть АО=х, тогда АС=2х.
ΔАВС ~ ΔDAO по двум углам ∠DAC=∠ВСА и ∠АВС=∠AOD=90°.
Тогда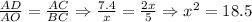
Из прямоугольного ΔАВС найдем катет АВ:
Значит в трапеции ABCD: AB=7, BC=5, CD=7.4, DA=7.4.