Вариант 2 Заданиесвыборомответа ( ).Рис. 1А1Рис. 1?А)АDC и ADB В)СDB и ABCС) ADB и DCBД) DKB и DCAА2Рис. 1 D?А) РDВВ) АDСС) АРСД) ВDСA3Рис. 1 иплоскость ADB?А) РВ) СС) АД) DA4Рис. 1 AВСи PDC?А) DВВ) DСС) PСД) ВAA5Рис. 1 PDC?А) DB, AC,DK. ABВ) KB, DA,DK. CPС) DP, DC,DM. CPД) DB, DC,DK. CBРис. 2А6Рис. 2 NC сплоскостью ABDА) D В) СС) АД) MА7Рис. 2 CDD1А) DВВ) DСС) ВСД) AВА8Плоскостиαиβпересекаютсяпопрямойс.Выберитевернуюзапись:А) α × β= сВ) α∩β= сС) α║β= сД) α∩β= СА9 1,2,3,4,5, 6 расположенныхнастержняхa,b,c.d ) 0 В) 1 С) 2 Д) 3Рис. 3А10Рис. 3Найдитеуголмеждупрямыми AD и DCА) 180º В) 60 ºС) 90 º Д) 45 ºА11Рис. 3Какрасполагаютсяпрямые DD1и AA1?А)параллельныВ)пересекаютсяС)перпендикулярныА12Рис. 3 и AD1А) D В) СС) АД) КА13Найдитерёбра,параллельныеграни DCC1D1А)АВ,ВВ1, A1 В1, AA1В)АD, ВC, A1 D1, B1С1С)АD, ВC, A1 D1, Заданиесвыборомответа ( ).Рис. 4А14Рис. 4) AD║ BC В) AB D ⊥1С1 С) DC ║ BC Д) DС⊥BA А15Рис. 4Укажитерёбра,1А) DА,ВC,СС1. ABВ)СB, DA,D1А1. C1А1С) DС,В1A1 ,BА. D1C1А16.?А)НетВ)ДаА17ОтрезокВD перпендикуляренплоскостиα. СD является::А)ПерпендикуляромВ)НаклоннойС)Проекциейнаклонной
S треугольника всегда = высота*основание к которому она проведена разделить это всё на два. (h*осн.)/2
1) высота - 6, основание 12, значит площадь - 12*6/2= 72/2=36 - Б
2)Если в треугольнике есть угол в 30 градусов, то сторона напротив него - в два раза меньше гипотенузы ( стороны напротив прямого=90 угла).
Тут гипотенуза = 12 значит сторона напротив угла равна 12/2 = 6. Чтобы найти вторую сторону используем теорему Пифагора.
a^2+b^2=c^2
где а и б - стороны, а с - гипотенуза. Подставим известное...
6^2+b^2=12^2
36+B^2=144
b^2=144-36
b^2=108
b =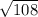
Площадь треугольника здесь - 6*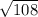 /2 = 3*
/2 = 3*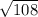 =18
=18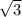 -в
-в
3)Опустим высоту. Найдём её тоже через свойство угла в 30 градусов и теорему пифагора. 16-4=12 значит высота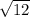 . в итоге.
. в итоге.
площадь=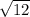 *6=6
*6=6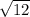 =12
=12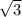 - в
- в
4)Наименьшая высота будет опущена к самой большой стороне, запомни. Опустим ее к стороне 20. Через формулы ( набери в инете среднее геометрическое, долго оформлять очень ) найдём, что x=12,8 - кусочек, которой получается в результате деления высотой стороны двадцать, который ближе к стороне 16. Аналогично найдём и кусочек, ближний к стороне 12. y=7,2. Высота равна корню произведения xy= 9,6 - высота - г
Построение сечения.
1. Проводим пряную ЕF до пересечения с продолжениями отрезков
СВ (F1) и СD (Е1). ЕF -линия пересечения секущей плоскости и плоскости основания.
2. Проводим прямую НF1, пересечение этой прямой с ребром ВВ1 -
точка G. GH - линия пересечения секущей плоскости и грани ВВ1С1С.
3. Соединим точки F и G. FG - линия пересечения секущей плоскости и грани АА1В1В.
4. Плоскости АВСD и А1В1С1D1 параллельны, значат линия НК пересечения секущей плоскости и грани А1В1С1D1 будет проходить через точку Н параллельно прямой ЕF.
5. Проводим прямую КЕ1, пересечение этой прямой с ребром DD1 -точка Р. КР -линия пересечения секущей плоскости и грани DD1C1C.
6. Соединим точки Р и Е. РЕ -линия пересечения секущей плоскости и грани АА1D1D.
Нахождение угла.
Угол между плоскостью сечения EFGHKP и плоскостью А1ВD -угол
A1RQ = α, образованный пересечением указанных плоскостей плоскостью, перпендикулярной к обеим плоскостям, то есть перпендикулярной к линии пересечения МN данных двух плоскостей.
Заметим, что этот угол равен углу А1ОС1, так как QL параллельна С10
(так как LО=С1Q, потому что EF - средняя линия прямоугольного треугольника АЕF и АL=LO=C1Q). Половина диагонали основания
(квадрата со стороной а) СО равна а*√2/2.
А тангенс угла С10С равен СС1/СО = а*2/а*√2 = √2.
По таблице тангенсов угол С10С ≈ 55°. Значит и симметричный с ним угол А1ОА =55°, их сумма равна 110°, а дополняющий эти два угла до развернутого искомый угол равен 180°-110°=70°.
ответ: угол между плоскостями FGНКРЕ и A1BD ≈ 70°.
ответ в приложенном рисунке.