Вариант 2
1. начертите три неколлинеарных вектора т”, пи k . постройте векторы, равные:
a. mi + 27
б. 2n - l
в. еті + 4k
г. зk – 2ті
2. на стороне kl квадрата mnkl лежит точка e так, что ke=el, o – точка
пересечения диагоналей. выразите векторы no, ne, em через векторы x=nm
и ў=nk.
3. в треугольнике mnk o – точка пересечения медиан. выразите вектор om
через векторы ä=nm и b=km.
4. в параллелограмме abcd точка m – середина стороны cd; n — точка на
стороне ad, такая, что аn: nd = 3: 4. выразите векторы cn и mn, nb, bd
через векторы b = вс иä = ab.
МД₁=6
Объяснение:
Искомым расстоянием от точки пересечения медиан М, до плоскости π является отрезок МД₁.
Обозначим высоты от стороны АС к плоскости π: В₁К, АЕ, СЕ₁. Соединим точки Е и Е₁. Получим трапецию ЕАСЕ₁. В₁К || АЕ || СЕ, так как они перпендикулярны плоскости π. По теореме Фалеса если параллельные прямые, пересекая стороны угла отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на второй стороне угла, поэтому если АВ₁=В₁С, то ЕК=КЕ₁. → В₁К – средняя линия трапеции ЕАСЕ₁.
В₁К=(ЕА+Е₁С)÷2=(2+5)÷2=7÷2=3,5
Проведём перпендикуляры В₁Н и КК₁ к стороне ВК₁, получили трапецию В₁КК₁В.
В₁Н делит ВК₁, что К₁Н=В₁К=3,5, тогда ВН=11–3,5=7,5.
Рассмотрим ∆ВВ₁Н, он прямоугольный, ВН и В₁Н – катеты, ВВ₁ – гипотенуза. Медианы треугольника, пересекаясь, точкой пересечения делятся на отрезки в отношении 2 : 1, начиная от вершины треугольника, поэтому ВМ : МВ₁=2 : 1 и по теореме Фалеса ДН : В₁Д=2 : 1. МД || ВН, и МД отсекает от ∆ВВ₁Н подобный ему ∆МВ₁Д. Стороны ∆ВВ₁Н имеют 3 части (2+1=3), а стороны ∆МВ₁Д – одну часть. Пусть МД=х, запишем пропорцию:
МД : ВН=1 : 3
Произведение крайних членов пропорции равно произведению средних:
МД•3=ВН•1
3х=7,5•1
3х=7,5
х=7,5÷3
х=2,5
ДД₁=В₁К=НК₁=3,5
МД₁=МД+ДД₁=2,5+3,5=6
Задание 1
ответ: Да, существует. Это правильный 8-ми угольник (см. картинку №1).
Объяснение:
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 135° × n
Отсюда выходит что:
135n = 180(n-2)
Находим n:
135n = 180n - 360
180n - 135n = 360
45n = 360
n = 360 ÷ 45
n = 8 (количество сторон правильного многоугольника)
Задание 2
ответ: Количество сторон правильного многоугольника = 12 (см. картинку №2).
Объяснение:
Пускай внутренний угол правильного многоугольника = x°
⇒ смежный с ним угол = 0,2x°
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол = 180°.
⇒ x + 0,2x = 180
1,2x = 180
x = 180 ÷ 1,2
x = 150° (внутренний угол выпуклого многоугольника)
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 150° × n
Отсюда выходит что:
150n = 180(n-2)
Находим n:
150n = 180n - 360
180n - 150n = 360
30n = 360
n = 360 ÷ 30
n = 12 (количество сторон правильного многоугольника)
Задание 3
а) ответ: Площадь многоугольника = 64 см².
Объяснение:
Правильный многоугольник, в котором n = 4 это КВАДРАТ.
Диаметр окружности d = 2r, где r - радиус
Известно что сторона квадрата a равна диаметру d вписанной в него окружности
⇒ d = a = 2r = 2×4 = 8 cm.
Площадь квадрата = a² = 8² = 64 cm²
б) ответ: Радиус вписанной окружности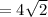
см.
Объяснение:
Известно что сторона квадрата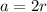
, где r - радиус вписанной окружности.
Так же известно что сторона квадрата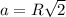
, где R - радиус описанной окружности ⇒
в) ответ: Периметр многоугольника = 16 см.
Объяснение:
Известно что сторона квадрата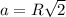
, где R - радиус описанной окружности
⇒
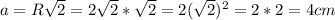
Периметр любого многоугольника P = n·a, где a - сторона многоугольника, n - количество его сторон.
⇒ P = 4 × 4 = 16 cm