AB = 10 ; BC = 20 .
Объяснение:
ABCD - параллелограмм => BC || AD => ∠MAD = ∠BMA (как внутренние накрест лежащие) => ΔABM - равнобедренный => AB = BM ;
BC || AD => ∠ADM = ∠CMD (как внутренние накрест лежащие) => ΔMCD - равнобедренный => MC = CD ;
ABCD - параллелограмм => AB = CD => AB = BM = MC = CD => M - середина BC => BC = 2 * AB ;
P (ABCD) = 2 * (AB + BC) ;
64 = 2 * (AB + 2*AB) ;
64 = 2 * 3*AB ;
6*AB = 64
AB = 64 / 6 = 10 = 10 ;
BC = 2 * AB ;
BC = 2 * 10 = 20 .
По свойству биссектрис треугольник ABM- равнобедренный AB=BM
DMC тоже равнобедренный треугольник. Т.к. DM биссектриса угла D, следовательно CD=MC.
Отсюда следует, что треугольник ABM=BMC.
AB=CD, т к ABCD параллелограмм
AD=BC=2AB
4AB=64
AB=64:4=16
AB=CD=16
AD=BC=2*16=32
AB = 10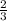 ; BC = 20
; BC = 20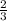 .
.
Объяснение:
ABCD - параллелограмм => BC || AD => ∠MAD = ∠BMA (как внутренние накрест лежащие) => ΔABM - равнобедренный => AB = BM ;
BC || AD => ∠ADM = ∠CMD (как внутренние накрест лежащие) => ΔMCD - равнобедренный => MC = CD ;
ABCD - параллелограмм => AB = CD => AB = BM = MC = CD => M - середина BC => BC = 2 * AB ;
P (ABCD) = 2 * (AB + BC) ;
64 = 2 * (AB + 2*AB) ;
64 = 2 * 3*AB ;
6*AB = 64
AB = 64 / 6 = 10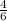 = 10
= 10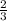 ;
;
BC = 2 * AB ;
BC = 2 * 10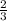 = 20
= 20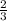 .
.
Объяснение:
По свойству биссектрис треугольник ABM- равнобедренный AB=BM
DMC тоже равнобедренный треугольник. Т.к. DM биссектриса угла D, следовательно CD=MC.
Отсюда следует, что треугольник ABM=BMC.
AB=CD, т к ABCD параллелограмм
AD=BC=2AB
4AB=64
AB=64:4=16
AB=CD=16
AD=BC=2*16=32