Верно ли, что каждой стороне первого треугольника можно найти сторону равную ему во втором, равном треугольнике?
Верно ли, что каждому углу первого треугольника можно найти угол, равный ему во втором, равном треугольнике?

Пусть меньшая сторона равна х см, тогда большая - (x+17) см.

Примем меньшую сторону за основание равнобедренного треугольника, а большую - за боковую сторону, тогда периметр треугольника

P = x + 2(x+17) = 3x + 34 = 47

3x = 13

x = 13/3 - сторона основания

см - боковая сторона

Примем теперь меньшую сторону за боковую сторону равнобедренного треугольника, а большую - за сторону основания

Боковые стороны равны 10 см, а сторона основания 10+17=27 см. Но так как не выполняется одно из неравенств треугольника: 10 + 10 > 27, то такой треугольник с сторонами 10 см, 10 см и 27 см не существует.

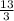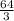ответ: см; 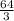см; см.

  Величина угла между  плоскостями  – угол, сторонами которого являются лучи, по которым эти плоскости пересекаются плоскостью, перпендикулярной ребру угла. 

Искомый угол –это угол DHC, образованный отрезками СН и DH (см. рисунок в приложении).

СН - высота ∆ АВС,   DC –⊥ плоскости ∆ АВС по условию, DH ⊥ АВ по т. о трёх перпендикулярах, 

плоскость  DHC перпендикулярна АВ.

СН как катет ∆ АНС, противолежащий углу 30º, равен половине  гипотенузы АС и равен а/2

Тангенс угла DHC=DC/HC=[(а√3):2]:a/2=√3.

Это тангенс угла, равного 60º.

Угол между плоскостью (ADB) и плоскостью (ACB)=60º.