Вершину правильного треугольника соединили отрезком с точкой, делящей противоположную сторону в отношении 7 : 8. в образовавшейся при этом два треугольника вписали круги, площадь одного из которых равна 81. найдите площадь второго круга.
Найдем, как связаны радиусы вписанных окружностей.
Пусть сторона правильного треугольника равна a.
Сначала нужно найти длину отрезка AD. Проще всего это сделать по теореме косинусов.
Посмотрим на треугольник ABD. В нем BD = 7/15 a, AB = a, угол B = 60 градусов.
Тогда ,
AD = 13/15 a
Периметр треугольника ACD = a + 8/15 a + 13/15 a = 36/15 a, треугольника ABD = a + 7/15 a + 13/15 a = 35/15 a.
С одной стороны, площадь треугольника - половина прооизведения высоты на сторону, с другой - половина произведения периметра на радиус списанной окружности. Если считать по первой формуле, получим, что S1/S2 = CD/DB = 8/7 (здесь индекс 1 соответствует треугольнику ACD). По второй: S1/S2 = (36*r1)/(35*r2).
Итак,
Площади кругов пропорциональны квадратам радиусов, поэтому площади относятся как 100 к 81.
Есдиственный вопрос, площадь какого из кругов дана. Отсюда и 2 ответа: 81*100/81=100 или 81*81/100=65.61
Найдем, как связаны радиусы вписанных окружностей.
Пусть сторона правильного треугольника равна a.
Сначала нужно найти длину отрезка AD. Проще всего это сделать по теореме косинусов.
Посмотрим на треугольник ABD. В нем BD = 7/15 a, AB = a, угол B = 60 градусов.
Тогда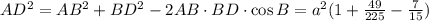 ,
,
AD = 13/15 a
Периметр треугольника ACD = a + 8/15 a + 13/15 a = 36/15 a, треугольника ABD = a + 7/15 a + 13/15 a = 35/15 a.
С одной стороны, площадь треугольника - половина прооизведения высоты на сторону, с другой - половина произведения периметра на радиус списанной окружности. Если считать по первой формуле, получим, что S1/S2 = CD/DB = 8/7 (здесь индекс 1 соответствует треугольнику ACD). По второй: S1/S2 = (36*r1)/(35*r2).
Итак,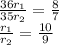
Площади кругов пропорциональны квадратам радиусов, поэтому площади относятся как 100 к 81.
Есдиственный вопрос, площадь какого из кругов дана. Отсюда и 2 ответа: 81*100/81=100 или 81*81/100=65.61
ответ: 100 или 65,61.