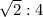Висота циліндра дорівнює 8 см, а діагональ осьового перерізу - 10 см. Знайдіть радіус циліндра. Висота циліндра дорівнює 8 см, а діагональ осьового перерізу - 10 см. Знайдіть радіус циліндра.
Единичный тетраэдр - треугольная пирамида, длина каждого ребра которой равна единице. Следовательно, пирамида МАВС - правильная, все ее грани - правильные треугольники.
Данное сечение - треугольник, высота которого равна высоте МО пирамиды, а основание - высоте АН основания пирамиды.
Основание О высоты правильной пирамиды - точка пересечения высот ( медиан, биссектрис) основания АВС.
АО=радиусу описанной окружности.
АО=R=a/√3=1/√3 (по формуле радиуса описанной окружности).
Пирамида правильная. значит, её основание –правильный треугольник, а боковые грани - равнобедренные треугольники. Если боковые грани правильной пирамиды наклонены под углом 60° к плоскости основания, ⇒ проекции равных наклонных - высот боковых граней, равны радиусу вписанной в основание окружности. НО=r=OK:sin60°
HO=OK:(√3/2)=4/√3
СН - высота АВС. ОС=2•ОН; CH=3•OH=12√3
АС=СН:sin60°=12√3):(√3/2)=24 см - сторона основания.
Апофема МН=ОН:cos60°=8/√3
S бок=h•p/2, где h- апофема, р - полупериметр основания.
S=( 8/√3)•3•24:2=288/√3=96√3 см²
Единичный тетраэдр - треугольная пирамида, длина каждого ребра которой равна единице. Следовательно, пирамида МАВС - правильная, все ее грани - правильные треугольники.
Данное сечение - треугольник, высота которого равна высоте МО пирамиды, а основание - высоте АН основания пирамиды.
Основание О высоты правильной пирамиды - точка пересечения высот ( медиан, биссектрис) основания АВС.
АО=радиусу описанной окружности.
АО=R=a/√3=1/√3 (по формуле радиуса описанной окружности).
По т.Пифагора из ∆ АМО высота
МО=√(AM²-AO²)=√(1-1/3)=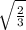
S ∆ MAH= MO•AH:2 =