Висота одного правильного трикутника дорівнює стороні другого правильного трикутника. Яке відношення площ цих трикутників? А) 1 : 4; Б) 3 : 4; В) 1 : 3; Г) 4 : 3.
Пусть ABCD - равнобедренная трапеция, AB = CD. Средняя линия трапеции = 12, т.е. BC + AD = 2*12 = 24. Угол А = 30 градусам.
Для любого четырехугольника, описанного около окружности справедливо: BC + AD = AB + CD 24 = 2* AB AB = 12.
Опустим высоту BH. Для прямоугольного треугольника известно, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, т.е. BH = AB : 2 = 12 : 2 = 6.
Радиус окружности, вписанной в равнобедренную трапецию, равен половине высоты, значит, r = BH : 2 = 6 : 2 = 3.
Доказательство:
Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.
Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.
Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что,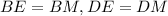 .
.
Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что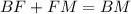 .
.
Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть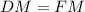 .
.
Учитывая доказанные равенства получаем,
Что требовалось доказать.
Для любого четырехугольника, описанного около окружности справедливо:
BC + AD = AB + CD
24 = 2* AB
AB = 12.
Опустим высоту BH. Для прямоугольного треугольника известно, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, т.е.
BH = AB : 2 = 12 : 2 = 6.
Радиус окружности, вписанной в равнобедренную трапецию, равен половине высоты, значит, r = BH : 2 = 6 : 2 = 3.
ответ: 3.