Внаклонной треугольной призме боковое ребро равно 10 см. площади двух боковых граней равны 30 и 40 см2, угод между ними прямой. найти площадь боковой поверхности призмы. с рисунком
Смотрим образовавшийся прямоугольный (т.к. медиана в равностороннем треугольнике является и высотой, и биссектрисой) треугольник: Т.к. она является и биссектрисой, то угол поделится пополам, т.е. будет равен = 30. Дальше воспользуемся тригонометрией, а именно косинусом (напомню, косинус - отношение прилежащего катета к гипотенузе): cos 30=√3/2 √3/2=9√3/x √3х=18√3 х=18 (см) - сторона треугольника. Если есть желание, можешь расковырять через теорему Пифагора, обозначив второй катет за х, а гипотенузу за 2х. ответ получится абсолютно тот же.
Т.к. она является и биссектрисой, то угол поделится пополам, т.е. будет равен = 30. Дальше воспользуемся тригонометрией, а именно косинусом (напомню, косинус - отношение прилежащего катета к гипотенузе):
cos 30=√3/2
√3/2=9√3/x
√3х=18√3
х=18 (см) - сторона треугольника.
Если есть желание, можешь расковырять через теорему Пифагора, обозначив второй катет за х, а гипотенузу за 2х. ответ получится абсолютно тот же.
Длина боковых сторон равнобедренного треугольника - 7 см, а длина его основания - 4 см.
Объяснение:
Запишем эту задачу с уравнения. Пусть a и b - боковые стороны равнобедренного треугольника, а c - его основание.
Прибавим разницу между суммой длин боковых сторон и основанием = равнобедренного треугольника:
Раскрываем скобки:
Учитываем тот факт, что бое=ковые стороны равнобедренного треугольника равны и длина каждой из них будет обозначаться a:
Делим длину сторон на их количество:
Теперь легко узнать основание равнобедренного треугольника:
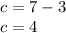
УДАЧИ! ОБРАЩАЙТЕСЬ!