Внутрішні односторонні кути при перетині двох паралельних прямих січною відносяться як 2:8. Знайди ці кути.

Известно, что диагональ в прямоугольном треугольнике является гипотенузой. Тогда мы можем найти периметр прямоугольного треугольника по формуле где a - любой катет, c - гипотенуза:

,

Для того, чтобы вынести число из под корня, нужно записать подкоренное выражение как произведение множителей таким образом, чтобы из одного можно было извлечь арифметический корень.

Разложим на множители число 74:

74=1*2*37,

Не из одного множителя нельзя извлечь арифметический корень, чтобы получить целое число.  Если разложить как 74=4*18,5, то выйдет:

, корень из 74 приблизительно равен 8,60 = 9

Таким образом,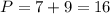

ответ: P прямоугольного треугольника приблизительно равен 16 см.

P.S. Возможно в условии задачи допущена ошибка, так как по указанным вводным точное значение найти не предстоит возможным. Необходимо перепроверить с первоисточником. Прикрепите фотографию.

1.  

∆АВС≈∆AMK по 3-ём углам (∠А-общий, ∠AMK=∠ABC как соответственные при секущей AB и MK║BC, ∠AKM=∠ACB как соответственные при секущей AC и MK║BC) ⇒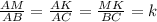

AM/AB=4/6=MK/BC=8/x      x=6·8:4=12 см - BC

AM/AB=4/6=AK/AC=9/y       y=6·9:4=13,5 см - AC

ответ: 12 см - BC и 13,5 см - AC

2.

По свойству медиан в треугольнике:

BO=8=2x ⇒ OK=x=4 см

AD=3х=24 ⇒ OD=x=8 см, а AO=2x=16 см

ответ: ОК=4; АО=16; ОD=8

3.

ВD - биссектриса ∆АВС ⇒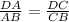

Пусть DA=x, тогда DC = 11-x

Составим пропорцию: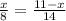

14x=88-8x

14x+8x=88

22x=88

x=4 см - сторона AD

11-4=7 cм- сторона DC

ответ: 4 см - сторона AD  и  7 cм- сторона DC