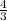Вокружность радиуса √2 см проведена хорда, длина которой составляет 1/3 диаметра. определите расстояние от центра окружности до этой хорда.(с рисунком, .)
Сделаем рисунок. Соединив хонцы хорды с центром окружности,
получим равнобедренный треугольник
с боковыми сторонами, равными радиусу окружности,
и основанием - данной в условии хордой. Радиус r по условию √2 см хорда АВ= D:3=2r:3=2√2):3 Проведем из центра окружности к хорде высоту ( медиану) h этого равнобедренного треугольника.
Найдем ее длину по т. Пифагора из прямоугольного треугольника АОМ,
где АО= r,
OM =h ,
AM = AB:2
h²=r²-АМ²
AМ={2√2):3}:2=√2):3 h²=(√2)²- { √2):3}² =2- 2/9 Приведем дробную часть уравнения к общему знаменателю: h²=(18-2):9=16/9 h=4/3 см
ответ: Расстояние от центра окружности до хорды 4/3 см
Так как линия проведенная из центра окружности, перпендикулярная хорде делит ее пополам, получаем прямоугольный треугольник, исходя из русунка во вложении найдем растояние от центра окружности до хорды:
Сделаем рисунок.
Соединив хонцы хорды с центром окружности,
получим равнобедренный треугольник
с боковыми сторонами, равными радиусу окружности,
и основанием - данной в условии хордой.
Радиус r по условию √2 см
хорда АВ= D:3=2r:3=2√2):3
Проведем из центра окружности к хорде высоту ( медиану) h этого равнобедренного треугольника.
Найдем ее длину по т. Пифагора из прямоугольного треугольника АОМ,
где АО= r,
OM =h ,
AM = AB:2
h²=r²-АМ²
AМ={2√2):3}:2=√2):3
h²=(√2)²- { √2):3}² =2- 2/9
Приведем дробную часть уравнения к общему знаменателю:
h²=(18-2):9=16/9
h=4/3 см
ответ: Расстояние от центра окружности до хорды 4/3 см
Так как линия проведенная из центра окружности, перпендикулярная хорде делит ее пополам, получаем прямоугольный треугольник, исходя из русунка во вложении найдем растояние от центра окружности до хорды:
ответ: