Вправильной треугольной призме все рёбра равны 4, через точки ac1 и середину т рёбра а1b1 проведена плоскость. а) докажите что сечение призмы указанной плоскостью является прямоугольный треугольник б) найдите тангенс угла между плоскостью сечения и плоскостью abc. ! ! к завтра нужно
Объяснение:
ЗАДАНИЕ 10
если <ВАС=120°, то ВС является основанием треугольника АВС, а АС и АВ - боковыми сторонами. Медиана АН, проведённая из вершины угла А к основанию ВС является ещё высотой и биссектрисой, которая образует два равных прямоугольных треугольника ВАН и САН, в которых АВ и АС - гипотенузы, а ВН, СН и медиана АН - катеты, поэтому <САН=<ВАН=120÷2=60° и <АНВ=<АНС=90°. Сумма острых углов прямоугольного треугольника составляет 90°, поэтому <АВН=<АСН=90–60=30°. Медиана-катет, лежащая напротив угла 30° равна половине гипотенузы поэтому АН=20÷2=10см
ОТВЕТ: АН=10см
ЗАДАНИЕ 11
а) Если АВ и СД параллельны, то <АСД=<KCN=110° и внутренний угол АВД= внешнему углу В
ABСД- четырёхугольник, при котором две противоположные стороны параллельны и 2 противоположных угла равны (по условиям), следовательно этот четырёхугольник - параллелограмм, поэтому АС || ВД
б) если провести отрезок АД, то получится равнобедренный треугольник АСД, в котором АД - основание, а АС = ВД. и являются боковыми сторонами, поэтому углы при основании САД и СДА равны. Сумма углов треугольника составляет 180°, поэтому <САД=<СДА=(180–110)÷2=70÷2=35°.
ОТВЕТ: углы ∆ДАС (САД=СДА)=35°
в) если можно использовать предыдущие данные, что АС=АД, то четырёхугольник АВСД- ромб, у которого все стороны равны, поскольку в задании а) мы выяснили, что АВСД- параллелограмм и если АС=АД,=АВ=ВД=18см, тогда периметр ромба=18×4=72см
ОТВЕТ: Р=72см
В треугольнике ABC его медианы AA1, BB1 и СС1 пересекаются в точке О. Середины отрезков OA, OB и OC обозначены соответственно A2, B2 и C2. Выразите периметр шестиугольника A2C1B2A1C2B1 через медианы ma = AA1, mb = BB1, mc = CC1.
Объяснение:
Медиана точкой пересечения делится на отрезки в отношении 2:1 ,считая от вершины ( см рисунок 1):
ОА=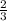 mа , ОВ=
mа , ОВ=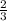 mb , ОС=
mb , ОС=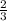 mc .
mc .
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон .Это отрезки :
А₂С₁ и А₁С₂ соответственно в ΔОАВ и ΔОАС ;
С₂В₁ и С₁В₂ соответственно в ΔОСА и ΔОАВ ;
А₂В₁ и А₁В₂ соответственно в ΔОАС и ΔОВС .
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
А₂С₁=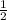 ОВ=
ОВ= 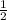 *
*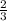 mb =
mb =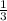 mb , А₁С₂ =
mb , А₁С₂ =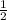 ОВ=
ОВ= 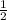 *
*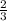 mb =
mb =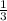 mb ;
mb ;
С₂В₁=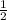 ОА=
ОА= 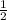 *
*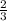 mа =
mа =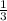 mа , С₁В₂ =
mа , С₁В₂ =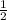 ОА=
ОА= 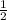 *
*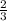 mа =
mа =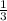 mа ;
mа ;
А₂В₁ =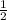 ОС=
ОС= 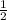 *
*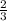 mс =
mс =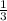 mс , А₁В₂ =
mс , А₁В₂ = 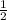 ОС=
ОС= 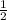 *
*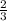 mс =
mс =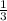 mс .
mс .
Р(шестиугольника)=2*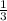 mb+2*
mb+2*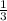 mа+2*
mа+2*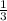 mс=
mс=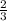 ( mа+ mb+mс)
( mа+ mb+mс)