Объяснение:
Площадь боковой поверхности прямого параллелепипеда:
S = Росн · ВВ₁
Росн = 2(AB + BC) = 2(1 + 7√3)
Проведем ВН⊥АС. ВН - проекция В₁Н на плоскость основания, значит
В₁Н⊥АС по теореме о трех перпендикулярах, ⇒
∠В₁НВ = 60° - линейный угол двугранного угла между плоскостями (В₁АС) и основанием.
ΔАВС: по теореме косинусов:
АС² = AB² + BC² - 2·AB·BC·cos∠B
AC² = 1 + 147 + 2 · 7√3 · √3/2 = 148 + 21 = 169
AC = 13
Sabc = 1/2 AB · BC · sin∠B = 1/2 · 7√3 · 1/2 =
Sabc = 1/2 AC · BH
ΔBB₁H:
tg∠B₁HB = BB₁ / BH
BB₁ = BH · tg60°
Объяснение:
Площадь боковой поверхности прямого параллелепипеда:
S = Росн · ВВ₁
Росн = 2(AB + BC) = 2(1 + 7√3)
Проведем ВН⊥АС. ВН - проекция В₁Н на плоскость основания, значит
В₁Н⊥АС по теореме о трех перпендикулярах, ⇒
∠В₁НВ = 60° - линейный угол двугранного угла между плоскостями (В₁АС) и основанием.
ΔАВС: по теореме косинусов:
АС² = AB² + BC² - 2·AB·BC·cos∠B
AC² = 1 + 147 + 2 · 7√3 · √3/2 = 148 + 21 = 169
AC = 13
Sabc = 1/2 AB · BC · sin∠B = 1/2 · 7√3 · 1/2 =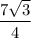
Sabc = 1/2 AC · BH
ΔBB₁H:
tg∠B₁HB = BB₁ / BH
BB₁ = BH · tg60°