Впрямоугольном треугольнике acb (угол с=90°) ав=10 см, угол авс=30°. с центром в точке а проведена окружность. каким должен быть ее радиус, чтобы: а) окружность касалась прямой вс в) окружность не имела общих точек с прямой вс с) окружность имела две общие точки с прямой вс ! соч по
Обозначим пирамиду МАВС, МО - высота пирамиды. МО перпендикулярна основанию пирамиды.
О - центр описанной окружности около основания АВС данной пирамиды.
Все углы правильного треугольника равны 60°. По т.синусов радиус АО описанной окружности равен
R=AO:2sin60°
Если условие задано верно и сторона основания равна 4, то:
Тогда по т.Пифагора из прямоугольного ∆ АМО высота
МО=√(AM²-AO²)=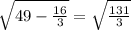
Но эта задача обычно задается со стороной основания, равной 4,5
Тогда условие задачи: В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания 4,5. Найдите высоту.
Для этого значения
R=4: 2√3/2=4,5:√3=1,5•√3
По т.Пифагора высота пирамиды
МО=√(МА²-АО²)=√(49-2,25•3)=6,5 (ед. длины)
138° : 2 = 69°
ответ: 69°.
2) 180° : (2 + 3 + 4) = 20° - 1 часть.
2 х 20° = 40°
3 х 20° = 60°
4 х 20 = 80°
ответ: 40°, 60°, 80°.
3) АВ = АС + ВС
ВС = АВ - АС = 17 - 9 = 8 (см)
ответ: ВС = 8 см.
4) 180° : (8 + 5 + 2) = 12° - 1 часть.
8 х 12° = 96°
5 х 12° = 60°
2 х 12° = 24°
180° - 96° = 84°
180° - 60° = 120°
180° - 24° = 156°
ответ: 84°, 120°, 156° - внешние углы треугольника.
5) Сумма смежных углов равна 180°.
х - один угол,
2х - другой угол.
х + 2х = 180
3х = 480
х = 180 : 3
х = 60° - первый угол.
60° · 2 = 120° - второй угол.
ответ: 60° и 120°.
6) 54 : (2 + 7) = 6 (см) - одна часть.
2 · 6 = 12 (см) - АК.
7 · 6 = 42 (см) - ВК.