№1. Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора: BC = = = =
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
DC = DB = a : sin45 =
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.
Вариант 1
№1. Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора: BC =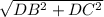 =
= 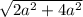 =
= 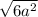 =
= 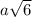
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
DC = DB = a : sin45 =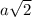
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.
DB = DC = BC =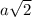
(Дальше долко)
(тут угол(HBC) равен 109,06°.на фото не видно, и поэтому подобрал на глаз. если что, можешь там поменять цифры и заново посчитать)
Рассмотрим четырехугольник GHBC. Значит сумма углов выпуклого четырехугольника равна 360°.
Отсюда следует уравнение:
360°=угол(HBC)+ угол(BCG)+угол(CGH)+угол(GHB)
И еще по рисунку видно что угол(CGH)=угол(HGI)+угол(IGC)
Так же угол(GHB)=угол(GHI)+угол(IHB)
Подставляем все это в уравнение
360°=угол(HBC)+угол(BCG)+угол(HGI)+угол(IGC)+угол(GHI)+угол(IHB)
Отсюда выходит такое уравнение:
угол(IGС)=360°-угол(HBC)+угол(BCG)+угол(HGI)+угол(GHI)+угол(IHB)=360°-42,71°-36,69°-68,09°-48,31°-42,71°-109,06°=12,43°
ответ: 12,43°