всем привет , у кого есть тетрадь по геометрии 8 класс (контрольные и самостоятельные работы )Беларусь . скиньте контрольную номер 1 оба варианта​

объяснение:

спершу знайдемо периметр мешого трикутника, сторони якого відомі:

Р = 3+5+7=15

потім поділимо периметр більшого трикутника на периметр меншого трикутника ( так дізнаємось у скільки разів більший трикутник ):

75:15= 5

трикутник більший у 5 разів, а отже

3*5=15

5*5=25

7*5=35

Також є другий б розвязування, через х:

нехай менший трикутник буде 3+5+7, а більший 3х+5х+7х, тоді

3+5+7=15,а 3х+5х+7х=75, тут так само 75:15= 5, - це шуканий х

відповідь та сама.

(Якщо не складно, поставте найкращу відповідь)

11.

Дано:

ΔАВС - равнобедренный

АС = ВС = 13

АВ = 10

Найти:

АС - высоту. опущенную на боковую сторону

СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.

По теореме Пифагора

АС² = CD² + AD²

13² = CD² + 5²

CD² = 13² - 5² = 144 = 12²

CD = 12

Площадь треугольника АВС

S = 0.5 CD · AB = 0.5 · 12 · 10 = 60

Площадь треугольника АВС можно также вычислить и так:

S = 0.5 BC · AE

откуда

АЕ = 2S : BC = 2 · 60 : 13 = 9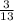 ≈ 9.23

АЕ = 9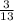 ≈ 9.23

12.

Дано:

MKNR - ромб

KR = 10 - 1-я диагональ ромба

MN = 12 - 2-я диагональ ромба

Найти:

МК - сторону ромба

Пусть О - точка пересечения диагоналей ромба.

Диагонали ромба делятся точкой пересечения пополам, поэтому

КО = 0,5 KR = 0.5 · 10 = 5

МО = 0,5 MN = 0.5 · 12 = 6

Диагонали ромба пересекаются под прямым углом, поэтому

КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.

По теореме Пифагора

МК² = КО² + МО²

МК² = 5² + 6² = 61

МК = √61 ≈ 7,81

Сторона ромба МК =√61 ≈ 7,81