Найдём диагональ d прямоугольника-основания призмы как гипотенузу в прямоугольном треугольнике, образованном сторонами основания и его диагональю. Она является проекцией диагонали призмы на основание, а также катетом в прямоугольном треугольнике, образованном катетом - ребром призмы (равным высоте призмы) , катетом - диагональю основания и гипотенузой - диагональю призмы.
d=
Прямоугольный треугольник, в котором есть внутренний угол 45°, является равнобедренным, поэтому высота призмы равна диагонали основания, как два катета в равнобедренном прямоугольном треугольнике.
Площадь боковой поверхности узнаем, вычислив периметр основания и умножив его на высоту призмы.
(∠В+∠С) -∠В=56, значит, ∠С=56°, смежный с этим углом внешний угол при вершине С равен 180°-56°=124°;
Если основанием является АС, то ∠А=56°, по свойству углов при основании в равнобедренном треугольнике. а внешний угол при вершине А тоже равен 124°.
Тогда ∠В=180°-2*56°=68°, и внешний при вершине В равен 180°-68°=112°
Если же основанием является АВ, т.е. ∠С - угол при вершине равнобедренного треугольника, то
∠А=∠В=(180°-56°)/2=62°, и соответственно углы, внешние: при вершинах А и В равны 180°-62°=118°, а при вершине С 124°
280 см²
Объяснение:
Найдём диагональ d прямоугольника-основания призмы как гипотенузу в прямоугольном треугольнике, образованном сторонами основания и его диагональю. Она является проекцией диагонали призмы на основание, а также катетом в прямоугольном треугольнике, образованном катетом - ребром призмы (равным высоте призмы) , катетом - диагональю основания и гипотенузой - диагональю призмы.
d=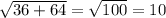
Прямоугольный треугольник, в котором есть внутренний угол 45°, является равнобедренным, поэтому высота призмы равна диагонали основания, как два катета в равнобедренном прямоугольном треугольнике.
Площадь боковой поверхности узнаем, вычислив периметр основания и умножив его на высоту призмы.
Sбок.=P·d=(6+8)·2·10=280 см²