Втреугольнике кнм кн=12, нм=9, мк=18. через точку а, лежащую на стороне нм, проведён перпендикуляр к биссекктрисе угла н, пересекающий сторону км в точке в. в каком отношении точка а делит сторону нм, если кс=2кв

Показать ответ

Ответ:

sharinaEl

28.03.2023 09:34

ответ:Это — четыре основных доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.

Объяснение:Доказательство с векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.

0,0(0 оценок)

Ответ:

kira183kira

28.03.2023 09:34

(см. объяснение)

Объяснение:

Первый

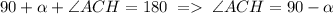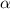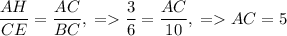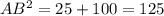Пусть ∠ECB=a. Тогда, т.к. ∠ACB=90°, то $90+\alpha+\angle ACH=180\;=\;\angle ACH=90-\alpha$ . Соответственно $\angle HAC=90-(90-\alpha)=\alpha$ . Значит треугольник AHC подобен треугольнику BEC по двум углам (∠AHC=∠BEC=90° и ∠ECB=∠HAC= $\alpha$ ). Из подобия следует, что $\dfrac{AH}{CE}=\dfrac{AC}{BC},\;=\dfrac{3}{6}=\dfrac{AC}{10},\;=AC=5$ . Тогда по теореме Пифагора для ΔABC: AB^2=25+100=125 .

Приведу решение, в котором используется только теорема Пифагора:

Пусть AC=x. AH=3, а BE=8. Тогда из прямоугольного треугольника AHC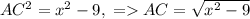 $AC^2=x^2-9,\;=AC=\sqrt{x^2-9}$ . Из прямоугольного треугольника BCE 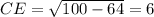$CE=\sqrt{100-64}=6$ . Значит 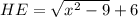$HE=\sqrt{x^2-9}+6$ . Проведем AF - высоту из точки A на BE. Тогда AFEH - прямоугольник => 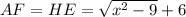$AF=HE=\sqrt{x^2-9}+6$ . По теореме Пифагора для прямоугольного треугольника AFB 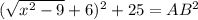$(\sqrt{x^2-9}+6)^2+25=AB^2$ . Но с другой стороны из прямоугольного треугольника ABC 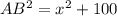AB^2=x^2+100 , т.е. получили уравнение 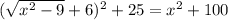$(\sqrt{x^2-9}+6)^2+25=x^2+100$ , откуда x=5, а значит 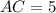AC=5 . 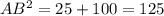Тогда AB^2=25+100=125 .