Решение: 1. Найдем катеты прямоугольного треугольника. Пусть x - 1 часть. Тогда 3х - 1 катет, 4х - второй катет. Решая уравнение по т. Пифагора, получим: 9x^2+16x^2=2500 25x^2=2500 x^2=100 x=-+10
-10 мы значение не берем по смыслу. Значит, x=10. Тогда 3х = 3*10 = 30(мм) 4х = 4*10 = 40(мм). 2. Если катет есть среднее пропорциональное для отрезка, делящаяся высотой, проведенной из вершины угла, и гипотенузы, то выразим сам этот отрезок: ac=a^2\c a - катет с - гипотенуза a с индексом с - отрезок. ac=900\50=18 А второй отрезок можем найти разностью между гипотенузой и этим отрезком: 50-18=32(мм). ответ: 18 и 32 мм
1. Найдем катеты прямоугольного треугольника. Пусть x - 1 часть. Тогда 3х - 1 катет, 4х - второй катет. Решая уравнение по т. Пифагора, получим: 9x^2+16x^2=2500
25x^2=2500
x^2=100
x=-+10
-10 мы значение не берем по смыслу. Значит, x=10.
Тогда 3х = 3*10 = 30(мм)
4х = 4*10 = 40(мм).
2. Если катет есть среднее пропорциональное для отрезка, делящаяся высотой, проведенной из вершины угла, и гипотенузы, то выразим сам этот отрезок:
ac=a^2\c
a - катет
с - гипотенуза
a с индексом с - отрезок.
ac=900\50=18
А второй отрезок можем найти разностью между гипотенузой и этим отрезком: 50-18=32(мм).
ответ: 18 и 32 мм
ответ: вторая высота равна либо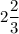
дм , либо 6 дм .
ΔАВС , АС=18 дм , АВ=12 дм , СМ ⊥ АВ , ВР ⊥ АС .
Одна из высот равна 4 дм .
Так как в условии не сказано, какая высота равна 4 дм , то рассмотрим два случая .
1) Пусть задана высота СМ=4 дм .
Запишем, чему равна площадь ΔАВС в двух вариантах.
S=0,5*AB*CM = 0,5*AC*BP ⇒ АВ*СМ=АС*ВР .
Заменим стороны и высоту известными числами .
12*4=18*ВР , 48=18*ВР , ВР=48:18=2 и 2/3 дм
2) Пусть задана высота ВР=4 дм .
Аналогично имеем АВ*СМ=АС*ВР , 12*СМ=18*4 , 12*СМ=72 ,
СМ=72:12=6 дм