Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
В задании фигура с указанными координатами неправильно названа - это параллелограмм. В любом случае диагональю фигуру разбить на 2 треугольника, Искомая площадь равна сумме двух треугольников. Треугольник АВС Точка А Точка В Точка С Ха Уа Хв Ув Хс Ус 2 -2 8 -4 8 8 Длины сторон: АВ ВС АС 6.32455532 12 11.66190379 Периметр Р = 29.98646, p = 1/2Р = 14.99323, Площадь определяем по формуле Герона: S = 36.
Треугольник АСД Точка А Точка С Точка Д Ха Уа Хс Ус Хд Уд 2 -2 8 8 2 10 АС СД АД 11.6619038 6.32455532 12 Периметр Р = 29.99, р = /2Р = 4.99 Площадь определяем по формуле Герона: S = 36. Итого площадь фигуры равна 36 + 36 = 72 кв.ед.
Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
ответ: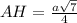
В любом случае диагональю фигуру разбить на 2 треугольника,
Искомая площадь равна сумме двух треугольников.
Треугольник АВС
Точка А Точка В Точка С
Ха Уа Хв Ув Хс Ус
2 -2 8 -4 8 8
Длины сторон:
АВ ВС АС
6.32455532 12 11.66190379
Периметр Р = 29.98646,
p = 1/2Р = 14.99323,
Площадь определяем по формуле Герона: S = 36.
Треугольник АСД
Точка А Точка С Точка Д
Ха Уа Хс Ус Хд Уд
2 -2 8 8 2 10
АС СД АД
11.6619038 6.32455532 12
Периметр Р = 29.99, р = /2Р = 4.99
Площадь определяем по формуле Герона: S = 36.
Итого площадь фигуры равна 36 + 36 = 72 кв.ед.