Формула площади параллелограмма: , так как прямоугольник - частный случай параллелограмма и его диагонали равны, то формула перепишется так:
Из площади найдём диагональ прямоугольника: (см).
Рассмотрим треугольник, образованный двумя половинками диагоналей и одной из сторон треугольника (выделен зелёным на рисунке). Так как мы имеем дело с прямоугольником, половинки диагоналей равны, значит треугольник равнобедренный. Так как угол между диагоналями равен 60°, то данный треугольник - равносторонний, ведь все углы равностороннего треугольника по 60°.
Значит ширина прямоугольника равна половине диагонали, то есть: (см).
Длину найдём по теореме Пифагора из треугольника образованного диагональю и двумя смежными сторонами прямоугольника: (см).
Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольникиМА2В2 и МА1В1подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
Формула площади параллелограмма: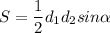 , так как прямоугольник - частный случай параллелограмма и его диагонали равны, то формула перепишется так:
, так как прямоугольник - частный случай параллелограмма и его диагонали равны, то формула перепишется так: 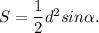
Из площади найдём диагональ прямоугольника: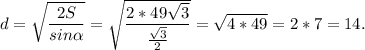 (см).
(см).
Рассмотрим треугольник, образованный двумя половинками диагоналей и одной из сторон треугольника (выделен зелёным на рисунке). Так как мы имеем дело с прямоугольником, половинки диагоналей равны, значит треугольник равнобедренный. Так как угол между диагоналями равен 60°, то данный треугольник - равносторонний, ведь все углы равностороннего треугольника по 60°.
Значит ширина прямоугольника равна половине диагонали, то есть: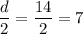 (см).
(см).
Длину найдём по теореме Пифагора из треугольника образованного диагональю и двумя смежными сторонами прямоугольника: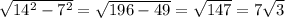 (см).
(см).
Так же длину можно было найти из площади: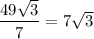 (см).
(см).
ответ: длина 7√3 см, ширина 7 см.