Вычисли стороны и площадь прямоугольника, если его диагональ равна 5√3 дм и образует с большей стороной угол 30 градусов.
Большая сторона = __ дм.
Меньшая сторона = __√__ дм.
Площадь = __√__ дм²​

ответ: 13

Пошаговое решение:

1) Если один из углов прямоугольного треугольника равен 60°, тогда его второй острый угол будет равен 30°.

2) Катет, лежащий против угла 30°, равен половине гипотенузы, т.к. синус угла 30° = 0.5, а в прямоугольном треугольнике синус угла - это отношение противолежащего ему катета к гипотенузе.

3) Катет, лежащий против угла 60°, равен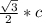 , где - гипотенуза.

4) Площадь прямоугольного треугольника равна полупроизведению его катетов. Отсюда: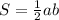 . Получаем уравнение:

Так как катет, прилежащий к углу 60°, равен половине гипотенузы (), то он равен 13.

1. Дано: КМРТ - трапеция, КМ=РТ, КТ=14 дм, МР=8 дм. МН - высота, МН=4 дм. Найти КМ.

Решение: проведем высоту РС.

МР=СН=8 дм.

ΔКМН=ΔРСТ по катету и гипотенузе, КН=СТ=(14-8):2=3 дм.

Рассмотрим ΔКМН - прямоугольный, КН=3 дм, МН=4 дм, значит КМ=5 дм (египетский треугольник).

ответ: 5 дм.

2. Дано: КМСТ - прямоугольник, Р=56 см, КТ-МК=4 см. Найти МТ.

Решение: МК+КТ=56:2=28 см.  Пусть КТ=х см, тогда МК=х-4 см.

Составим уравнение: х+х-4=28;  2х=32;  х=16.

КТ=16 см;  МК=16-4=12 см. Тогда по  теореме Пифагора

МТ=√(16²+12²)=√(256+144)=√400=20 см.

(или просто: МТ=20 см, т.к. МК:КТ=12:16=3:4;  МКТ - египетский треугольник)

ответ: 20 см.