Исходя из суммы углов треугольника, в треугольнике RPQ угол при верщине R = 30 градусам. Что означает, что в прямоугольном треугольнике RPQ катет равен половине гипотенузы, то есть RP=2*PS=36.
Аналогично в треугольнике RPQ угол Q=30 градусов, а значит гипотенуза PQ=2*RP=72.
Следовательно QS=PQ-PS=72-18=54
Старое решение:
Исходя из суммы углов треугольника, угол при верщине Q = 30 градусам. Тогда из треугольника tg60=RS/PS, а tg30=RS/QS
Диагональ параллелепипеда можно найти по формуле: √a²+b²+c², где
a,b,c - наши измерения. Если подставить значения, то выдет √50=5√2 см
далее, если посмотреть на основание, то это прямоугольник со сторонами 3 и 4 см. по теореме Пифагора найдем диагональ или гипотенузу треугольника ABD: она равна 5 см.
из треугольника CBD: мы знаем CD=5√2; BD=5; BC= 5 по условию
BD=BC, значит треугольник CBD - равнобедренный, один из углов 90
QS=54
Объяснение:
Новое решение.
Исходя из суммы углов треугольника, в треугольнике RPQ угол при верщине R = 30 градусам. Что означает, что в прямоугольном треугольнике RPQ катет равен половине гипотенузы, то есть RP=2*PS=36.
Аналогично в треугольнике RPQ угол Q=30 градусов, а значит гипотенуза PQ=2*RP=72.
Следовательно QS=PQ-PS=72-18=54
Старое решение:
Исходя из суммы углов треугольника, угол при верщине Q = 30 градусам. Тогда из треугольника tg60=RS/PS, а tg30=RS/QS
RS=tg60*PS
RS=tg30*QS
tg60*PS=tg30*QS -> QS=(tg60*PS)/tg30=tg60*ctg30*PS
т.к. tg a * ctg b =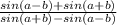
тогда Q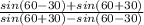S=
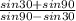*PS=
*PS=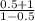
*PS=(1.5/0.5)*PS=3*PS
QS=3*18=54
Внизу.
Объяснение:
Диагональ параллелепипеда можно найти по формуле: √a²+b²+c², где
a,b,c - наши измерения. Если подставить значения, то выдет √50=5√2 см
далее, если посмотреть на основание, то это прямоугольник со сторонами 3 и 4 см. по теореме Пифагора найдем диагональ или гипотенузу треугольника ABD: она равна 5 см.
из треугольника CBD: мы знаем CD=5√2; BD=5; BC= 5 по условию
BD=BC, значит треугольник CBD - равнобедренный, один из углов 90
значит оставшиеся два равны по 45 градусов.
ответ: 45 градусов; 5√2 см