Проведем две высоты в трапеции, как приведено на рисунке. Отрезок, заключенный между высотами, по теореме Фалеса будет одним и тем же, то есть равным 6 см, значит оставшаяся часть - это 20 см. Если за x обозначить одну из частей, тогда 20 - x будет второй фрагмент этих 20 см.
Рассматривая прямоугольные треугольники и взяв на вооружение тот факт, что высота в данной трапеции будет одинаковой, можно решить уравнение:
Подставив это значение в , мы получим 92.16, а извлекая корень, получится 9.6
Расстояние от точки до плоскости есть перпендикуляр, опущенный из этой точки к плоскости. Следовательно АА₁⊥α, ВВ₁⊥α (смотри прикрепленный рисунок). Поскольку прямые АА₁ и ВВ₁ перпендикулярны плоскости α, то между собой они параллельны и образуют одну плоскость (через две параллельные прямые проходит плоскость и при чем только одна). Назовем ее β. Отрезок АВ тоже лежит в плоскости β, т. к. имеет с ней две общие точки (Если две точки прямой (отрезка) лежат в данной плоскости, то и вся прямая (отрезок) лежит в данной плоскости). Плоскость β пересекает плоскость α по прямой А₁В₁. Опустим из точки М перпендикуляр на плоскость α. ММ₁ будет параллельна прямым АА₁ и ВВ₁. Точка М₁ - точка пересечения ММ₁ с плоскостью α - будет лежать на прямой А₁В₁. (Это доказывается от противного. Если точка М₁ не лежит на прямой А₁В₁, то ММ₁ пересекает плоскость β. Поскольку ММ₁║АА₁, то и АА₁ тоже будет пересекать плоскость β. Получаем противоречие, т. к. АА₁ лежит в плоскости β. Значит Точка М₁ лежит на отрезке А₁В₁.) В плоскости β получаем четырехугольник АВА₁В₁, у которого две противоположные стороны параллельны. Следовательно этот четырехугольник - трапеция с основаниями АА₁ и ВВ₁. Так как основания трапеции перпендикулярны боковой стороне, то трапеция является прямоугольной. ММ₁ - средняя линия, т.к. М - середина отрезка АВ и параллельна основаниям. Значит и точка М₁ середина стороны А₁В₁. ответ: ММ₁ = 8 см.
9.6
Объяснение:
Проведем две высоты в трапеции, как приведено на рисунке. Отрезок, заключенный между высотами, по теореме Фалеса будет одним и тем же, то есть равным 6 см, значит оставшаяся часть - это 20 см. Если за x обозначить одну из частей, тогда 20 - x будет второй фрагмент этих 20 см.
Рассматривая прямоугольные треугольники и взяв на вооружение тот факт, что высота в данной трапеции будет одинаковой, можно решить уравнение:
Подставив это значение в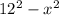
, мы получим 92.16, а извлекая корень, получится 9.6
Следовательно АА₁⊥α, ВВ₁⊥α (смотри прикрепленный рисунок).
Поскольку прямые АА₁ и ВВ₁ перпендикулярны плоскости α, то между собой они параллельны и образуют одну плоскость (через две параллельные прямые проходит плоскость и при чем только одна). Назовем ее β.
Отрезок АВ тоже лежит в плоскости β, т. к. имеет с ней две общие точки (Если две точки прямой (отрезка) лежат в данной плоскости, то и вся прямая (отрезок) лежит в данной плоскости).
Плоскость β пересекает плоскость α по прямой А₁В₁.
Опустим из точки М перпендикуляр на плоскость α.
ММ₁ будет параллельна прямым АА₁ и ВВ₁.
Точка М₁ - точка пересечения ММ₁ с плоскостью α - будет лежать на прямой А₁В₁.
(Это доказывается от противного. Если точка М₁ не лежит на прямой А₁В₁, то ММ₁ пересекает плоскость β. Поскольку ММ₁║АА₁, то и АА₁ тоже будет пересекать плоскость β. Получаем противоречие, т. к. АА₁ лежит в плоскости β. Значит Точка М₁ лежит на отрезке А₁В₁.)
В плоскости β получаем четырехугольник АВА₁В₁, у которого две противоположные стороны параллельны. Следовательно этот четырехугольник - трапеция с основаниями АА₁ и ВВ₁.
Так как основания трапеции перпендикулярны боковой стороне, то трапеция является прямоугольной.
ММ₁ - средняя линия, т.к. М - середина отрезка АВ и параллельна основаниям. Значит и точка М₁ середина стороны А₁В₁.
ответ: ММ₁ = 8 см.