Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла. Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке. Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей. Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов. Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов. Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48. Можно было бы и далее продолжать таким но мы замечаем закономерность. Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле: , где n - число лучей кратное 3. Пробуем вычислить по этой формуле:
Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла. Так считать долго, можно увидеть формулу для прямого расчёта:
По этой формуле можно считать для любого количества лучей, кратное трём.
Это утверждение соответствует ромбу и квадрату, но квадрат – это разновидность ромба, поэтому:
ответ: 3) ромб.
2. Один угол прямой и диагонали биссектрисы.
Диагонали - биссектриссы – это свойство ромба.
Но прямой угол у ромба есть только в случае, если этот ромб является квадратом.
ответ: 4) квадрат.
3. Противоположные стороны равны.
Это свойство любого параллелограмма.
ответ: 1) параллелограмм
4. Смежные стороны равны
Так как все противоположные четырехугольники это или параллелограмм или разновидности параллелограмма, то у них у всех противоположные стороны попарно равны.
Если смежные стороны равны, то получим что все стороны равны.
Четырехугольник у которого все стороны равны – это ромб.
ответ: 3) ромб
5. Диагонали делят на равные прямоугольные треугольники
Это свойство ромба. Диагонали ромба пересекаясь, образуют 4 прямых угла, и точкой пересечения делаться пополам. Получим что 4 полученных треугольника равны как прямоугольные треугольники с равными катетами и гипотенузами (все стороны роста равны)
ответ: 3) ромб.
6. Диагонали делят на равнобедренные треугольники
Это свойство прямоугольника. Диагонали прямоугольника равны и точкой пересечения деляться пополам. Получим что все полудиагонали равны, тогда 4 образованные треугольники равнобедренные.
ответ: 2) прямоугольник
7.Диагональ делит на равные прямоугольные треугольники
Это свойство прямоугольника. Всё углы прямоугольника прямые, а противоположные стороны равны. Тогда полученные треугольники равны как прямоугольные треугольники с равными катетами.
ответ: 2) прямоугольник.
8. Диагонали перпендикулярны и равны
Диагонали перпендикулярны – это свойство ромба.
Но диагонали равны – это свойство прямоугольника. Квадрат является разновидностью ромба и прямоугольника одновременно, тогда данное свойство – свойство квадрата
ответ: 4) квадрат
9. Все углы равны
В 4-угольнике сумма всех углов равна 360°. Если все они равны, то все они равны 360°÷4=90°. Все углы равны 90° – это свойство прямоугольника.
Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
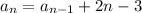, где n - число лучей кратное 3.
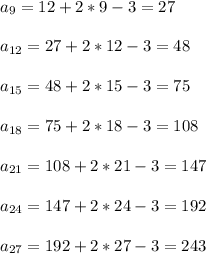
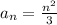
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле:
Пробуем вычислить по этой формуле:
Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла.
Так считать долго, можно увидеть формулу для прямого расчёта:
По этой формуле можно считать для любого количества лучей, кратное трём.
1.Диагонали перпендикулярны.
Это утверждение соответствует ромбу и квадрату, но квадрат – это разновидность ромба, поэтому:
ответ: 3) ромб.
2. Один угол прямой и диагонали биссектрисы.
Диагонали - биссектриссы – это свойство ромба.
Но прямой угол у ромба есть только в случае, если этот ромб является квадратом.
ответ: 4) квадрат.
3. Противоположные стороны равны.
Это свойство любого параллелограмма.
ответ: 1) параллелограмм
4. Смежные стороны равны
Так как все противоположные четырехугольники это или параллелограмм или разновидности параллелограмма, то у них у всех противоположные стороны попарно равны.
Если смежные стороны равны, то получим что все стороны равны.
Четырехугольник у которого все стороны равны – это ромб.
ответ: 3) ромб
5. Диагонали делят на равные прямоугольные треугольники
Это свойство ромба. Диагонали ромба пересекаясь, образуют 4 прямых угла, и точкой пересечения делаться пополам. Получим что 4 полученных треугольника равны как прямоугольные треугольники с равными катетами и гипотенузами (все стороны роста равны)
ответ: 3) ромб.
6. Диагонали делят на равнобедренные треугольники
Это свойство прямоугольника. Диагонали прямоугольника равны и точкой пересечения деляться пополам. Получим что все полудиагонали равны, тогда 4 образованные треугольники равнобедренные.
ответ: 2) прямоугольник
7.Диагональ делит на равные прямоугольные треугольники
Это свойство прямоугольника. Всё углы прямоугольника прямые, а противоположные стороны равны. Тогда полученные треугольники равны как прямоугольные треугольники с равными катетами.
ответ: 2) прямоугольник.
8. Диагонали перпендикулярны и равны
Диагонали перпендикулярны – это свойство ромба.
Но диагонали равны – это свойство прямоугольника. Квадрат является разновидностью ромба и прямоугольника одновременно, тогда данное свойство – свойство квадрата
ответ: 4) квадрат
9. Все углы равны
В 4-угольнике сумма всех углов равна 360°. Если все они равны, то все они равны 360°÷4=90°. Все углы равны 90° – это свойство прямоугольника.
ответ: 2) прямоугольник.
10. Диагонали точкой пересечения делятся пополам
Это свойство любого параллелограмма.
ответ: 1) параллелограмм.