Если ссылаетесь на рисунок в условии задания, этот рисунок следует приложить. Но данная задача понятна и без рисунка.
Высоты опущены из одной вершины. В параллелограмме более длинной является та высота, что проведена к стороне меньшей длины. Площадь параллелограмма равна произведению его высоты на сторону, к которой она проведена. Раз высота, равная 6, более длинная, она проведена к более короткой стороне.
S=6*9=54 Площадь этого параллелограмма можно найти и произведением другой высоты на большую сторону.
1) Все стороны ромба ABCD равны, поэтому каждая равна 53/4.
2) Диагонали AC и BD ромба ABCD взаимно перпендикулярни и по свойству параллелограмма точкой O пересечения делятся пополам.Поэтому половины диагоналей ромба (образующие прямой угол) также относятся как 2:7, т.е. АО:ОВ = 2:7.
3) Пусть t - длина некоторого отрезка. Тогда по теореме Пифагора
Значит, АО=
BO=
4) Площадь ромба равна половине произведения диагоналей. А с др. стороны, она равна произведению стороны на высоту к этой стороне. Отсюда
Если ссылаетесь на рисунок в условии задания, этот рисунок следует приложить.
Но данная задача понятна и без рисунка.
Высоты опущены из одной вершины. В параллелограмме более длинной является та высота, что проведена к стороне меньшей длины.
Площадь параллелограмма равна произведению его высоты на сторону, к которой она проведена.
Раз высота, равная 6, более длинная, она проведена к более короткой стороне.
S=6*9=54
Площадь этого параллелограмма можно найти и произведением другой высоты на большую сторону.
S=h*10
h=S:10
h=54:10=5,4
1) Все стороны ромба ABCD равны, поэтому каждая равна 53/4.
2) Диагонали AC и BD ромба ABCD взаимно перпендикулярни и по свойству параллелограмма точкой O пересечения делятся пополам.Поэтому половины диагоналей ромба (образующие прямой угол) также относятся как 2:7, т.е. АО:ОВ = 2:7.
3) Пусть t - длина некоторого отрезка. Тогда по теореме Пифагора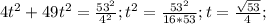
Значит, АО=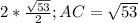
BO=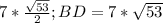
4) Площадь ромба равна половине произведения диагоналей. А с др. стороны, она равна произведению стороны на высоту к этой стороне. Отсюда