Высота правильной треугольной пирамиды равна 6см, а двугранный угол между боковой гранью и плоскостью основания пирамиды равен 30градусов. Найдите обьем пирамиды
4. Путь первый из полученных углов равен тогда второй равен а третий равен Так как вместе они составляют развернутый угол, то
Образованные углы равны
6. При пересечении двух прямых образуются две пары равных углов (или четыре равных прямых угла). Рассматривая пару смежных углов и сумма которых равна получаем:
а)
Складывая полученные уравнения, находим откуда из второго уравнения
б)
Подставляя значение из первого уравнения во второе, находим откуда
в) Так как сумма пары смежных углов равна речь идет о паре острых вертикальных углов,
1. Внешний угол тр-ка равен сумме двух не смежных с ним углов. Их отношение друг к другу равно 1:4, то есть они равны Х и 4*Х градусов. Итак Х+4*Х=5*Х=15°. Отсюда Х=3°. Значит наибольший из этих углов равен 3*4=12° 2. Окружность равна 360°. Дуга в 7/18 окружности равны 360*7/18=140°. Вписанный угол равен половине градусной меры дуги, на которую он опирается, то есть 70°. 3. Для того, чтобы четырёхугольник был описанным, необходимо и достаточно, чтобы он был выпуклым и имел равные суммы противоположных сторон. У нашего четырехугольника стороны равны Х, 6*Х, 9*Х. Тогда Х+9*Х = 6*Х+Y и каждая из этих равных сумм равна половине периметра четырехугольника, то есть = 10. Тогда Х= 10-9=1. Стороны равны: 1, 6, 9 и 4 (10-6). Значит большая сторона равна 9.
4.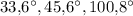
6. а)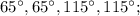 б)
б) 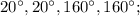 в)
в) 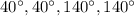
7.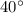
Объяснение:
4. Путь первый из полученных углов равен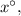 тогда второй равен
тогда второй равен 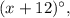 а третий равен
а третий равен 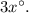 Так как вместе они составляют развернутый угол, то
Так как вместе они составляют развернутый угол, то 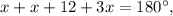
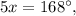
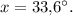
Образованные углы равны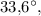
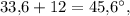
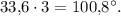
6. При пересечении двух прямых образуются две пары равных углов (или четыре равных прямых угла). Рассматривая пару смежных углов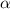 и
и 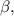 сумма которых равна
сумма которых равна 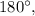 получаем:
получаем:
а)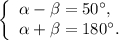
Складывая полученные уравнения, находим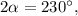
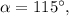 откуда из второго уравнения
откуда из второго уравнения 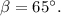
б)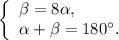
Подставляя значение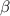 из первого уравнения во второе, находим
из первого уравнения во второе, находим 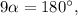
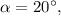 откуда
откуда 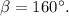
в) Так как сумма пары смежных углов равна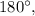 речь идет о паре острых вертикальных углов,
речь идет о паре острых вертикальных углов, 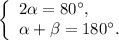
Из первого уравнения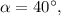 тогда из второго
тогда из второго 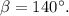
7. Пусть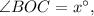 тогда
тогда 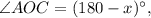 а его половина
а его половина 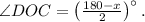 Значит
Значит 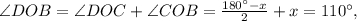
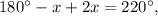

2. Окружность равна 360°. Дуга в 7/18 окружности равны 360*7/18=140°. Вписанный угол равен половине градусной меры дуги, на которую он опирается, то есть 70°.
3. Для того, чтобы четырёхугольник был описанным, необходимо и достаточно, чтобы он был выпуклым и имел равные суммы противоположных сторон. У нашего четырехугольника стороны равны Х, 6*Х, 9*Х. Тогда Х+9*Х = 6*Х+Y и каждая из этих равных сумм равна половине периметра четырехугольника, то есть = 10. Тогда Х= 10-9=1. Стороны равны: 1, 6, 9 и 4 (10-6). Значит большая сторона равна 9.