Пусть a - основание равнобедренного треугольника, l - биссектриса, r - радиус вписанной окружности, b - боковая сторона. Выразим площадь треугольника через радиус вписанной окружности: Биссектриса в равнобедренном треугольнике, проведённая к основанию, является и медианой, и высотой, поэтому: Приравняем теперь обе формулы: . Найдём по теореме Пифагора боковую сторону b: . У нас известен периметр, поэтому мы можем сложить все известные стороны и найти таким образом радиус вписанной окружности: Осталось найти длину круга: ответ:
Выразим площадь треугольника через радиус вписанной окружности:
Биссектриса в равнобедренном треугольнике, проведённая к основанию, является и медианой, и высотой, поэтому:
Приравняем теперь обе формулы:
Найдём по теореме Пифагора боковую сторону b:
У нас известен периметр, поэтому мы можем сложить все известные стороны и найти таким образом радиус вписанной окружности:
Осталось найти длину круга:
ответ:
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть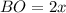
см и 
см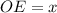, тогда 
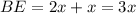, что по условию он равен 9 см.
Следовательно,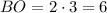
см и 
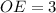см
Аналогично, пусть теперь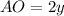
см и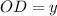 
, тогда 
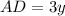и по условию равен 12 см
Таким образом,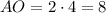
см и 
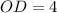см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника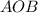
По теореме Пифагора из прямоугольного треугольника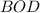
Тогда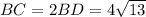
см
Из прямоугольного треугольника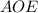
по теореме Пифагора
Тогда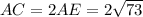
см
ответ:
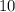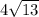см;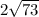 
см; 
см.