Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника АВС, пересекаются в точке О, причем угол ВОС равен 120 ͦ . Найдите угол ВАС.
1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒ ⇒
см
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны
Вторая задача. Порассуждаем немного. Для того, чтобы ребра пирамиды, в основании которой лежит прямоугольный треугольник, могли быть равными, их проекции должны быть равными. Такое может быть только если основание высоты пирамиды находится в центре гипотенузы прямогольного треугольника. Тогда два ребра имеют проекцию на гипотенузе, третье - медиане треугольника и все три наклонных и проекции оказываются равными. Задача из тех, что можо назвать удобными для решения: стороны рассматриваемых треугольников из числа Пифагоровых троек, т.е. стороны в которых образуют группу прямоугольных треугольников.
По открытой еще древними математиками истине, данные числа удовлетворяют уравнению x² + y² = z² Таковы, например: x = 3 , y = 4 , z = 5 или x = 5 , y = 12 , z = 13 Таких троек немало. Вот несколько, которые полезно помнить. (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15) ( две подчеркнутые использованы в решении задачи.
Вот и в этой задаче встречаются две таких тройки. Одна - высота пирамиды , половина основания и боковое ребро составляют
тройку 12, 5 - катеты, 13 - гипотенуза. Поэтому без вычисления можно сказать, что гипотенуза основания равна 2*5. Что касается второго катета основания - гипотенуза равна 10, один катет 6, второй обязательно будет 8 см. Т.е. стороны основания отосятся как 3:4:5 (6:8:10) ответ: Второй катет основания равен 8 см.
Но можно пользоваться и теоремой Пифагора
Рисунок очень простой. Нарисовать прямоугольный треугольник ( так, чтобы он был похож на лежащий на плоскости). Из центра гипотенузы возвести высоту, соединить вершину с углами основания, нарисовать проекцию третьего ребра ( медиана основания)
1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒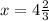 ⇒
⇒
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны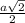
КО=МН=АВ=а
Р (КМНО=2(МН+КМ)=2a+2•(a√2/2)=a•(2+√2)
В первой задаче получаются несуразные дроби.
Вторая задача.
Порассуждаем немного.
Для того, чтобы ребра пирамиды, в основании которой лежит прямоугольный треугольник, могли быть равными, их проекции должны быть равными. Такое может быть только если основание высоты пирамиды находится в центре гипотенузы прямогольного треугольника. Тогда два ребра имеют проекцию на гипотенузе, третье - медиане треугольника и все три наклонных и проекции оказываются равными.
Задача из тех, что можо назвать удобными для решения: стороны рассматриваемых треугольников из числа Пифагоровых троек, т.е. стороны в которых образуют группу прямоугольных треугольников.
По открытой еще древними математиками истине, данные числа удовлетворяют уравнению x² + y² = z²
Таковы, например: x = 3 , y = 4 , z = 5 или x = 5 , y = 12 , z = 13
Таких троек немало. Вот несколько, которые полезно помнить.
(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15) ( две подчеркнутые использованы в решении задачи.
Вот и в этой задаче встречаются две таких тройки.
Одна - высота пирамиды , половина основания и боковое ребро составляют
тройку 12, 5 - катеты, 13 - гипотенуза. Поэтому без вычисления можно сказать, что гипотенуза основания равна 2*5.
Что касается второго катета основания - гипотенуза равна 10, один катет 6, второй обязательно будет 8 см. Т.е. стороны основания отосятся как 3:4:5
(6:8:10)
ответ: Второй катет основания равен 8 см.
Но можно пользоваться и теоремой Пифагора
Рисунок очень простой. Нарисовать прямоугольный треугольник ( так, чтобы он был похож на лежащий на плоскости). Из центра гипотенузы возвести высоту, соединить вершину с углами основания, нарисовать проекцию третьего ребра ( медиана основания)