Як побудувати прямокутний трикутник за катетом і протилежним гострим кутом? ( відправляйте фото з вже вирішеним прикладом у якому наглядно показано, що ви використовували циркуль )
Требуется найти площадь параллелограмма по известным данным.
Дано: ABCD параллелограмм, AB = 14 см, диагональ равна стороне, ∠A = 60°.
Найти: S.
Решение.
1) Покажем, что большая диагональ параллелограмма не может быть равна стороне.
В параллелограмме против большего угла лежит большая диагональ.
Сумма углов, прилежащих к одной стороне параллелограмма равна 180° (как односторонние углы при параллельных прямых и секущей).
Тогда один из этих углов острый, а другой - тупой.
Большая диагональ параллелограмма лежит против тупого угла.
Если большая диагональ параллелограмма равна его стороне, то получается равнобедренный треугольник с двумя равными углами при основании, которые являются тупыми. Чего не может быть.
Следовательно, в нашей задаче меньшая диагональ равна стороне параллелограмма.
2) По данным в задаче.
В параллелограмме ABCD ∠A = 60°, диагональ BD равна стороне AB:
BD = AB = 14 см.
ΔABD равнобедренный.
В равнобедренном треугольнике углы при основании равны.
∠ADB = 60°.
Из суммы углов треугольника следует, что ∠ABD = 60°, тогда треугольник равносторонний, сторона AD = 14 см.
(То есть параллелограмм является ромбом).
3) На этом этапе уже можно найти площадь параллелограмма ABCD, но так как просят решить задачу без применения синуса угла (и других тригонометрических функций), найдем ее другим .
Площадь параллелограмма равна произведению основания на высоту.
Найдем высоту параллелограмма.
Проведем в ΔABD высоту BH.
В равнобедренном треугольнике высота является и медианой.
Тогда AH = 14 см : 2 = 7 см.
Из прямоугольногоΔABH (∠AHB = 90°) найдем катет BH.
Высота параллелограмма см.
4) Зная высоту BH и основание AD параллелограмма, найдем его площадь.
Площадь параллелограмма равна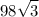 см².
см².
Объяснение:
Требуется найти площадь параллелограмма по известным данным.
Дано: ABCD параллелограмм, AB = 14 см, диагональ равна стороне, ∠A = 60°.
Найти: S.
Решение.
1) Покажем, что большая диагональ параллелограмма не может быть равна стороне.
В параллелограмме против большего угла лежит большая диагональ.
Сумма углов, прилежащих к одной стороне параллелограмма равна 180° (как односторонние углы при параллельных прямых и секущей).
Тогда один из этих углов острый, а другой - тупой.
Большая диагональ параллелограмма лежит против тупого угла.
Если большая диагональ параллелограмма равна его стороне, то получается равнобедренный треугольник с двумя равными углами при основании, которые являются тупыми. Чего не может быть.
Следовательно, в нашей задаче меньшая диагональ равна стороне параллелограмма.
2) По данным в задаче.
В параллелограмме ABCD ∠A = 60°, диагональ BD равна стороне AB:
BD = AB = 14 см.
ΔABD равнобедренный.
В равнобедренном треугольнике углы при основании равны.
∠ADB = 60°.
Из суммы углов треугольника следует, что ∠ABD = 60°, тогда треугольник равносторонний, сторона AD = 14 см.
(То есть параллелограмм является ромбом).
3) На этом этапе уже можно найти площадь параллелограмма ABCD, но так как просят решить задачу без применения синуса угла (и других тригонометрических функций), найдем ее другим .
Площадь параллелограмма равна произведению основания на высоту.
Найдем высоту параллелограмма.
Проведем в ΔABD высоту BH.
В равнобедренном треугольнике высота является и медианой.
Тогда AH = 14 см : 2 = 7 см.
Из прямоугольногоΔABH (∠AHB = 90°) найдем катет BH.
Высота параллелограмма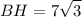 см.
см.
4) Зная высоту BH и основание AD параллелограмма, найдем его площадь.
Площадь параллелограмма равна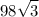 см².
см².
Расстояние AC = 13 см.
Объяснение:
Требуется найти расстояние от центра окружности до точки, лежащей на касательной к этой окружности.
Дано: окружность, т.A центр окружности, радиус 5 см, CB касательная, т.B - точка касания, CB = 12 см.
Найти: расстояние AC.
Решение.
Радиус, проведенный в точку касания, перпендикулярен касательной.
1) Проведем в окружности радиус AB.
Тогда AB = 5 см, ∠ABC = 90° (так как радиус проведен в точку касания B).
2) ΔABC прямоугольный, AC является гипотенузой треугольника (как сторона, лежащая против прямого угла), катеты AB = 5 см, BC = 12 см.
Найдем гипотенузу AC по т.Пифагора:
квадрат гипотенузы равен сумме квадратов катетов.
AC² = AB² + BC² = 5² + 12² = 25 + 144 = 169 = 13².
AC = 13 см.
Расстояние AC = 13 см.