Який вид трикутника якщо один з його зовнішніх кутів дорівнює 35°

1. Прямоугольный треугольник Треугольник называется прямоугольным, если у него есть прямой угол. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны – катетами.

2. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

3. Доказать, что гипотенуза больше катета В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. Во-первых, если знать тот факт, что напротив большего угла всегда лежит большая сторона, и два непрямых угла прямоугольного треугольника острые, то доказательство будет выглядеть совсем просто.

4. Сумма острых углов прямоугольного треугольника равна 90 градуса.

5. Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.

Решение с ответом:

AB = 12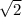 см

BC = 20 см

A = 45 градусов

BM - h

------------------------

СМ = ? см

Высота BM является перпендикуляром, опущенным на AC.

Т.е угол BMA и угол BMC - прямоугольные ( 90 градусов)

расс-им прямоугольный треугольник ABM:

угол BAM = 45 градусов (из условия)

угол  BMA = 90 градусов (BM - высота)

Найдем угол ABM по Теореме о сумме углов треугольника:

180 - (BAM + BMA) = 180 - (90 + 45) = 45 градусов.

Прямоугольный треугольник ABM является равнобедренным, его катеты равны м-у собой.

AM = BM

Гипотенуза у треугольника - AB, она равна 12 корень из 2 ()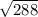

Из Теоремы Пифагора (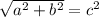) выходит, что квадрат равных м-у собой катетов a и b равен 144, корень из 144 - 12.

т.е AM = BM = 12 см.

расс-им треугольник BMC:

угол BMC - также прямоугольный.

BM = 12 см (по решению)

BC = 20 cм (из условия)

Катет CM = ?  см

Найдем его из Обратной Теоремы пифагора:

см

ОТРЕЗОК CM РАВЕН 16 СМ.