" Дано куб АВСDА1В1С1D1. Вычислить величину угла между векторами АВ1 и А1D с векторного метода (отметьте прямые АВ1 и А1D соответствующими векторами). Подсказка: воспользуйтесь формулой нахождения угла между векторами. "
Объяснение:
векторный
Пусть ребро куба а. Введем прямоугольную систему координат как показано на чертеже. Координаты точек
А(а ;0; 0) , В(0;0;а) , , =√((-a)²+0²+a²)=a√2 ;
А(а ;0; a) , D(a;a;0) , , =√(0²+a²+(-a)²)=a√2 .
Скалярное произведение можно вычислить двумя
-по определению ;
-используя координаты .
Получаем ,
2a²* = - а² ,
⇒ угол между векторами равен 120° .
Углом между двумя пересекающимися прямыми называется величина наименьшего из плоских углов, образованных этими прямыми ⇒ угол между прямыми АВ₁ и А₁D равен 60° .
по т. косинусов.
Достроим куб ( фактически до 2-го этажа).
Перенесем вектор как показано на чертеже, для совмещения начал данных векторов. Найдем угол между векторами из ΔА₁DB₂ по т. косинусов . Найдем длины отрезков
- А₁В₂=А₁D , какдиагонали квадрата , по т. Пифагора √(а²+а²)=а√2.
- DB₂ , как диагональ прямоугольного параллелепипеда с измерениями а, а,2а ; DB₂ =√(а²+а²+4а²)=а√6.
DB₂²= А₁В₂² + А₁D²-2*А₁В₂*А₁D* cos( А₁В₂;А₁D),
6а²=2а²+2а²-2*а√2*а√2* cos( А₁В₂;А₁D),
2*а√2*а√2* cos( А₁В₂;А₁D)=-2а²,
cos( А₁В₂;А₁D)=-1/2 ⇒ угол между отрезками А₁В₂;А₁D равен 120°. Тогда угол между прямыми АВ₁ и А₁D равен 60° (180° -120°=60° ) .
694. Используем формулу для радиуса вписанной окружности прямоугольного треугольника. r=p-c, где p - полупериметр. p-c=(a+b+c)/2-c=(a+b-c)/2. d=2r=(a+b-c)=m-c
696. Воспользуемся свойством описанного четырехугольника о том, что суммы противоположных сторон равны, т.е. AB+CD=BC+AD. Т.к. ABCD - параллерограмм, то AB=CD и BC=AD. Получаем, что 2AB=2BC, а значит AB=BC=CD=AD, т.е. ABCD - ромб
697. Возьмем центр вписанной окружности и разобьем четырехугольник на треугольники отрезками между центром окружности и вершинами многоугольника. Для каждого треугольника применим формулу площади: S=a*h/2, где a - сторона многоугольника, а h- высота из центра на эту сторону, т.е. радиус. Просуммируем и получим, что S=P*r/2=pr, что и требовалось доказать.
" Дано куб АВСDА1В1С1D1. Вычислить величину угла между векторами АВ1 и А1D с векторного метода (отметьте прямые АВ1 и А1D соответствующими векторами). Подсказка: воспользуйтесь формулой нахождения угла между векторами. "
Объяснение:
векторный
Пусть ребро куба а. Введем прямоугольную систему координат как показано на чертеже. Координаты точек
А(а ;0; 0) , В(0;0;а) ,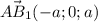
, 
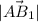=√((-a)²+0²+a²)=a√2 ;
А(а ;0; a) , D(a;a;0) ,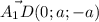
, 
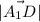=√(0²+a²+(-a)²)=a√2 .
Скалярное произведение можно вычислить двумя
-по определению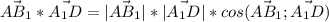
;
-используя координаты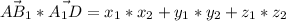
.
Получаем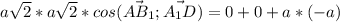
,
2a²*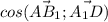
= - а² ,
Углом между двумя пересекающимися прямыми называется величина наименьшего из плоских углов, образованных этими прямыми ⇒ угол между прямыми АВ₁ и А₁D равен 60° .
по т. косинусов.
Достроим куб ( фактически до 2-го этажа).
Перенесем вектор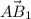
как показано на чертеже, для совмещения начал данных векторов. Найдем угол между векторами 
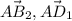из ΔА₁DB₂ по т. косинусов . Найдем длины отрезков
- А₁В₂=А₁D , какдиагонали квадрата , по т. Пифагора √(а²+а²)=а√2.
- DB₂ , как диагональ прямоугольного параллелепипеда с измерениями а, а,2а ; DB₂ =√(а²+а²+4а²)=а√6.
DB₂²= А₁В₂² + А₁D²-2*А₁В₂*А₁D* cos( А₁В₂;А₁D),
6а²=2а²+2а²-2*а√2*а√2* cos( А₁В₂;А₁D),
2*а√2*а√2* cos( А₁В₂;А₁D)=-2а²,
cos( А₁В₂;А₁D)=-1/2 ⇒ угол между отрезками А₁В₂;А₁D равен 120°. Тогда угол между прямыми АВ₁ и А₁D равен 60° (180° -120°=60° ) .
694. m-c
Объяснение:
694. Используем формулу для радиуса вписанной окружности прямоугольного треугольника. r=p-c, где p - полупериметр. p-c=(a+b+c)/2-c=(a+b-c)/2. d=2r=(a+b-c)=m-c
696. Воспользуемся свойством описанного четырехугольника о том, что суммы противоположных сторон равны, т.е. AB+CD=BC+AD. Т.к. ABCD - параллерограмм, то AB=CD и BC=AD. Получаем, что 2AB=2BC, а значит AB=BC=CD=AD, т.е. ABCD - ромб
697. Возьмем центр вписанной окружности и разобьем четырехугольник на треугольники отрезками между центром окружности и вершинами многоугольника. Для каждого треугольника применим формулу площади: S=a*h/2, где a - сторона многоугольника, а h- высота из центра на эту сторону, т.е. радиус. Просуммируем и получим, что S=P*r/2=pr, что и требовалось доказать.