З точки M, що лежить поза колом, проведено до кола дві дотичні MA і MB; де A і B - точки дотику, кут MBA = 60.Знайдіть відстань від точки M до центра кола, якщо радіус кола дорівнює 10 см.

Объяснение:

Пусть дан ΔАВС, В - вершина треугольника, АС - основание ΔАВС,

АВ =ВС, ∠А и ∠С - углы при основании.

1)  Внешний угол при вершине равнобедренного ΔАВС (обозначим его как β)  и внутренний ∠В  - смежные углы, и их сумма равна 180° .

Значит, внешний угол β = 180° - ∠В.

2) сумма углов треугольника = 180 °. Следовательно ,

∠А + ∠ В + ∠С = 180°, откуда ∠ В = 180° - ∠А - ∠С, но т.к.  ΔАВС - равнобедренный, и значит, ∠А = ∠С, получаем:

∠ В = 180° - 2∠А

Подставим это выражение в формулу для внешнего угла β, получим:

β = 180° - 180° +2∠А

β= 2∠А, ч. т. д.

68. По данным на рисунке найдите площадь .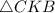

- - -Дано :

ΔСКВ - прямоугольный (∠С = 90°).

СК - высота (СК⊥АВ).

АК = 4, КВ = 16.

Найти :Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.

Следовательно,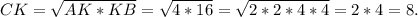

Площадь прямоугольного треугольника равна половине произведения его катетов.

Следовательно,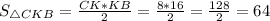 ед².

ответ :

64 ед².

- - -

70. ABCD - прямоугольник. Найдите .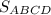

- - -Дано :

Четырёхугольник ABCD - прямоугольник.

АС - диагональ.

HD⊥АС.

HD = 6, АН = 9.

Найти :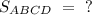

Решение :Прямоугольник - это параллелограмм, все углы которого прямые.

Следовательно ∠D = 90°.

Рассмотрим ΔACD - прямоугольный.

В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.

Следовательно,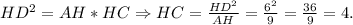

Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.

Следовательно,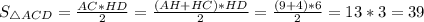 ед².

Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.

Тогда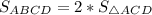 = 2*39 ед² = 78 ед².

ответ :

78 ед².