З точки М, що лежить поза колом, проведено до кола дві дотичні МА і МВ; де А і В – точки дотику, кут МВА = 6о°. Знайдіть відстань від точки М до центра кола, якщо радіус кало дорівнює 10 см.

На стороне AB остроугольного треугольника ABC(CB не равно AC) как на диаметре построена полуокружность пересекающая высотку cs в точке N, CS = 20, NS = 17, H - точка пересечения высот треугольника ABC. Найдите CH

Объяснение:

1.) Тк Н- точка пересечения высот CS и ВН  Δ ABC, то точка М лежит на окружности, для которой АВ –диаметр , т.к ∠ВМА=90°.

2.) ΔSАС ∼  ΔMHC по двум углам ( общему ∠С,  ∠НМС=∠АSC=90°), поэтому сходственные стороны пропорциональны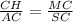  

или  АС*МС=СН*SC  .

3.) Достроим  SN ( часть перпендикуляра СS) до пересечения с окружностью .  Хорда КN ⊥AB, значит КS=SN=17.  Поэтому

КС= SC +KS =20+17=37      ,  NC= SC-SN=20-17=3 .  По теореме о секущих , проведенных из точки С :  NC*KC=MC*AC        , 3*37=MC*AC  .

4.)  АС*МС=СН*SC       , 3*37=СН*20     , СН=5,55

Параллельный перенос задается формулами

\begin{gathered} < var > x'=x+a;\\ y'=y+b;\\ z'=z+c < /var > \end{gathered}

<var>x

′

=x+a;

y

′

=y+b;

z

′

=z+c</var>

Так как при параллельном переносе точка А(-2;3;5) переходит в точку А1(1;-1;2), то

\begin{gathered} < var > 1=-2+a;\\ -1=3+b;\\ 2=5+c < /var > \end{gathered}

<var>1=−2+a;

−1=3+b;

2=5+c</var>

\begin{gathered} < var > a=1+2;\\ b=-1-3;\\ c=2-5 < /var > \end{gathered}

<var>a=1+2;

b=−1−3;

c=2−5</var>

\begin{gathered} < var > a=3;\\ b=-4;\\ c=-3 < /var > \end{gathered}

<var>a=3;

b=−4;

c=−3</var>

Данный параллельный перенос задается формулами

\begin{gathered} < var > x'=x+3;\\ y'=y-4;\\ z'=z-3 < /var > \end{gathered}

<var>x

′

=x+3;

y

′

=y−4;

z

′

=z−3</var>

Поэтому точка В(-4;-3;1) перейдет в точку c координатами

\begin{gathered} < var > x'=-4+3;\\ y'=-3-4;\\ z'=1-3 < /var > \end{gathered}

<var>x

′

=−4+3;

y

′

=−3−4;

z

′

=1−3</var>

\begin{gathered} < var > x'=-1;\\ y'=-7;\\ z'=-2 < /var > \end{gathered}

<var>x

′

=−1;

y

′

=−7;

z

′

=−2</var>

т.е. В1(-1;-7;-2)